
【题目】已知椭圆![]() 的实轴长为4,焦距为
的实轴长为4,焦距为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线l经过点![]() 且与椭圆C交于不同的两点M,N(异于椭圆的左顶点),设点Q是x轴上的一个动点.直线QM,QN的斜率分别为
且与椭圆C交于不同的两点M,N(异于椭圆的左顶点),设点Q是x轴上的一个动点.直线QM,QN的斜率分别为![]() ,
,![]() ,试问:是否存在点Q,使得
,试问:是否存在点Q,使得![]() 为定值?若存在.求出点Q的坐标及定值;若不存在,请说明理由.
为定值?若存在.求出点Q的坐标及定值;若不存在,请说明理由.
【答案】(1)![]() ;(2)在x轴上存在点
;(2)在x轴上存在点![]() ,使得
,使得![]() 为定值
为定值![]() .
.
【解析】
(1)根据实轴长为4,焦距为![]() 直接代入即可
直接代入即可
(2)当直线l与x轴垂直时,它与椭圆只有一个交点,不满足题意;所以直线l的斜率k存在,设直线l的方程为![]() ,把它和椭圆方程联立,利用韦达定理求出两根之和与两根之积,代入到
,把它和椭圆方程联立,利用韦达定理求出两根之和与两根之积,代入到![]() 中,令对应项系数成比例即可.
中,令对应项系数成比例即可.
解:(1)设椭圆C的半焦距为c.
因为椭圆C的长轴长为4,焦距为![]() ,
,
所以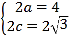 ,
,
解得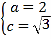 .则
.则![]() .
.
故椭圆C的标准方程为![]()
故答案为:![]() .
.
(2)假设存在满足条件的点![]() ,
,
当直线l与x轴垂直时,它与椭圆只有一个交点,不满足题意;所以直线l的斜率k存在,设直线l的方程为![]() .
.
联立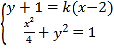 ,
,
得![]() ,
,![]() .
.
设点![]() ,
,![]() ,
,
则![]() ,
,![]()
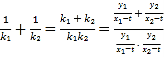
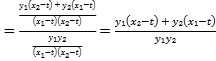
![]()
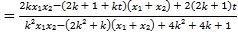
![]() ,
,
要使![]() 为定值.则需满足
为定值.则需满足![]() ,
,
解得![]() .
.
此时![]() .
.
所以在x轴上存在点![]() ,使得
,使得![]() 为定值
为定值![]()


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】某医院有内科医生8名,外科医生6名,现选派4名参加抗击新冠肺炎疫情医疗队,其中
(1)甲、乙两人至少有一人参加,有多少种选法?
(2)队中至少有一名内科医生和一名外科医生,有几种选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在其定义域内存在单调递减区间.
在其定义域内存在单调递减区间.
(1)求f(x)的单调递减区间;
(2)设函数![]() ,(e是自然对数的底数).是否存在实数a,使g(x)在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
,(e是自然对数的底数).是否存在实数a,使g(x)在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三台县某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的![]() 天内,西红柿市场售价与上市时间的关系为
天内,西红柿市场售价与上市时间的关系为![]() ;西红柿的种植成本与上市时间的关系为
;西红柿的种植成本与上市时间的关系为![]() .认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?最大收益是多少?(注:市场售价各种植成本的单位:元/
.认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?最大收益是多少?(注:市场售价各种植成本的单位:元/![]() ,时间单位:天)
,时间单位:天)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有10所学校,每所都选派若干名男生和若干名女生举行跳棋比赛,同一学校的选手不比赛,不同学校的选手不论男女在两人之间都要进行一场比赛. 在两个男生或两个女生之间的比赛总局数与男生和女生之间的比赛总局数与男生和女生之间的比赛总局数至多相差1,而男生的总人数和女生的总人数也至多相差1. 求证:至少有7所学校选派的男生和女生人数相同.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C.若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题
均为假命题
D.命题![]() :“
:“![]() ,使得
,使得![]() ”,则非
”,则非![]() :“
:“![]() ,
,![]() ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com