
已知定义在R上的奇函数 f(x)有最小正周期2,且当x∈(0,1)时, f(x)= .
.
(1) 求 f(x)在[-1,1]上的解析式;
(2) 证明: f(x)在(0,1)上是减函数.
(1)解:只需求出 f(x)在x∈(-1,0)和x=±1,x=0时的解析式即可,因此,要注意应用奇偶性和周期性,当x∈(-1,0)时,-x∈(0,1).
∵ f(x)是奇函数,∴ f(x)=-f(-x)=- =-
=-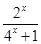 ,
,
由f(0)=f(-0)=-f(0),且f(1)=f(-2+1) =f(-1)=-f(1),
得f(0)=f(1)=f(-1)=0.
∴在区间[-1,1]上有
(2)证明:当x∈(0,1)时, f(x)=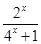 .
.
设0<x1<x2<1,f(x1)-f(x2)= -
- =
= .
.
∵0<x1<x2<1,∴2x2-2x1>0,2x1+x2-1>0,∴f(x1)-f(x2)>0,即f(x1)>f(x2),
故 f(x)在(0,1)上单调递减
【解析】略


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
| 1 |
| b |
| 1 |
| a |
查看答案和解析>>
科目:高中数学 来源:大连二十三中学2011学年度高二年级期末测试试卷数学(理) 题型:选择题
已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函
数,则( ).
A.  B.
B.

C.  D.
D.

查看答案和解析>>
科目:高中数学 来源:2012届浙江省高二下学期期末考试理科数学试卷 题型:选择题
已知定义在R上的奇函数 ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函
数,若方程 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则
 ( )
( )
(A) (B)
(B) (C)
(C)  (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com