
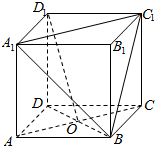
 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.分析 (1)转换底面求三棱锥B1-A1BC1的体积.
(2)取A1C1的中点E,连接NE,BE,证明NEBM是平行四边形,可得MN∥BE,即可证明MN∥平面A1BC1;
解答 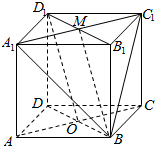 解:(1)解:正方体ABCD-A1B1C1D1,各棱长为1
解:(1)解:正方体ABCD-A1B1C1D1,各棱长为1
三棱锥B1-A1BC1的体积=三棱锥B-A1B1C1的体积=$\frac{1}{3}×1×1×1$=$\frac{1}{3}$.
(2)证明:取A1C1的中点M,连接BM,则
∵M,O分别为B1D1,BD的中点,
∴BO平行且等于MD1,
∴BOD1M是平行四边形,
∴MB∥OD1,
∵MB?平面A1BC1,MB?平面A1BC1,
∴OD1∥平面A1BC1;
点评 本题考查直线与平面平行的判定,考查三棱锥B1-A1BC1的体积,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com