
如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=a,AD=2a,PA⊥平面ABCD,PA=a.

(1)求证:PC⊥CD;
(2)求点B到直线PC的距离.
|
证明:(1)取AD的中点E,连AC,CE, 则ABCE是正方形,△CED为等腰直角三角形. ∴AC⊥CD,∵PA⊥平面ABCD,∴AC为PC在平面ABCD上的射影,∴PC⊥CD; 解:(2)连BE交AC于O,则BE⊥AC, 又BE⊥PA,AC∩PA=A,∴BE⊥平面PAC. 过O作OH⊥PC于H,连BH,则BH⊥PC. ∵PA=a,AC= ∵BO= |
|
(1)要证PC与CD垂直,只要证明AC与CD垂直,可按实际情形画出底面图形进行证明.(2)从B向直线PC作垂直,可利用△PBC求高,但需求出三边,并判断其形状(事实上,这里的∠PBC=90°);另一种重要的思想是:因PC在平面PAC中,而所作BH为平面PAC的斜线,故关键在于找出B在平面PAC内的射影,因平面PAC处于“竖直状态”,则只要从B作“水平”的垂线,可见也只要从B向AC作垂线便可得其射影. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
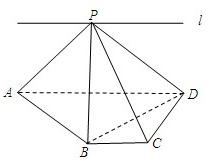 如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
如图,ABCD为直角梯形,∠C=∠CDA=90°,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.
如图,ABCD为直角梯形,∠DAB=∠ABC=90°,AB=BC=1,AD=2,PA⊥平面ABCD,PA=1.查看答案和解析>>
科目:高中数学 来源: 题型:
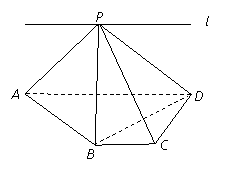
(14分)如图,ABCD为直角梯形,∠C=∠CDA=![]() ,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
,AD=2BC=2CD,P为平面ABCD外一点,且PB⊥BD.
⑴ 求证:PA⊥BD;
(2) 若![]() 与CD不垂直,求证:
与CD不垂直,求证:![]() ;
;
⑶ 若直线l过点P,且直线l∥直线BC,试在直线l上找一点E,
使得直线PC∥平面EBD.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省高三数学中等生强化练习(7)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年高考数学小题限时训练试卷(12)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com