练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知命题

    p1:函数y=2x-2-x在R上为增函数,

    p2:函数y=2x+2-x在R上为减函数,

    则在命题q1:p1∨p2,q2:p1∧p2,q3:(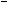p1)∨p2和q4:p1∧(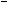p2)中,真命题是(　　)

    (A)q1,q3　　 (B)q2,q3　　 (C)q1,q4　　 (D)q2,q4

     

    C

    【解析】方法一:函数y=2x-2-x是一个增函数与一个减函数的差,故函数y=2x-2-x在R上为增函数,p1是真命题;

    而对p2:y'=2xln2-ln2=ln2×(2x-),

    当x∈[0,+∞)时,2x≥,又ln2>0,所以y'≥0,函数单调递增;同理得当x∈

    (-∞,0)时,函数单调递减,故p2是假命题.由此可知,q1真,q2假,q3假,q4真.

    方法二:p1是真命题同方法一;由于2x+2-x≥2=2,故函数y=2x+2-x在R上存在最小值,故这个函数一定不是R上的单调函数,故p2是假命题.由此可知, q1真,q2假,q3假,q4真.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：选择题

    计算:lg-lg+lg7=　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（二）第一章第二节练习卷（解析版） 题型：选择题

    下面四个条件中,使a>b成立的充分而不必要条件是(　　)

    (A)a>b+1 (B)a>b-1 (C)a2>b2 (D)a3>b3

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（三）第一章第三节练习卷（解析版） 题型：解答题

    已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x满足不等式x2+2ax+2a≤0,若命题“p∨q”是假命题,求a的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（三）第一章第三节练习卷（解析版） 题型：选择题

    下列说法中,不正确的是(　　)

    (A)命题p:?x∈R,sinx≤1,则p:?x∈R,sinx>1

    (B)在△ABC中,“A>30°”是“sinA>”的必要不充分条件

    (C)命题p:点(,0)为函数f(x)=tan(2x+)的一个对称中心;命题q:如果|a|=1,|b|=2,<a,b>=120°,那么b在a方向上的投影为1,则(p)∨(q)为真命题

    (D)命题“在△ABC中,若sinA=sinB,则△ABC为等腰三角形”的否命题为真命题

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（七）第二章第四节练习卷（解析版） 题型：解答题

    已知函数f(x)=a-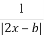是偶函数,a为实常数.

    (1)求b的值.

    (2)当a=1时,是否存在n>m>0,使得函数y=f(x)在区间[m,n]上的函数值组成的集合也是[m,n],若存在,求出m,n的值,否则,说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（七）第二章第四节练习卷（解析版） 题型：选择题

    若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是(　　)

    (A)(-∞,2] (B)[2,+∞)

    (C)[-2,+∞) (D)(-∞,-2]

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（一）第一章第一节练习卷（解析版） 题型：选择题

    已知集合M={x|y=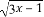},N={x|y=log2(x-2x2)},则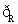(M∩N)=(　　)

    (A)(,) (B)(-∞,)∪[,+∞)

    (C)[0,] (D)(-∞,0]∪[,+∞)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷（解析版） 题型：解答题

    如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.

    求证:(1)BC1⊥AB1.

    (2)BC1∥平面CA1D.

     

    查看答案和解析>>

    同步练习册答案