练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．如图，半径为4的球O中有一内接圆往，则圆柱的侧面积最大值是32π．

    分析 设出圆柱的上底面半径为r，球的半径与上底面夹角为α，求出圆柱的侧面积表达式，求出最大值

    解答 解：∵设圆柱的上底面半径为r，球的半径与上底面夹角为α，则r=4cosα，圆柱的高为8sinα，
    ∴圆柱的侧面积为：32πsin2α，当且仅当α=$\frac{π}{4}$时，sin2α=1，圆柱的侧面积最大，
    ∴圆柱的侧面积的最大值为：32π．
    故答案为：32π．

    点评 本题是基础题，考查球的内接圆柱的知识，圆柱的侧面积的最大值的求法，考查计算能力，常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    12．已知函数$f（x）=\left\{\begin{array}{l}x+2{\;}^{\;}（x＜0）\\{x^2}{\;}^{\;}{\;}^{\;}（0≤x＜2）\\ \frac{1}{2}x{\;}^{\;}{\;}^{\;}（x≥2）\end{array}\right.$．
    （1）求f（f（2））的值
    （2）画出此函数的图象．
    （3）若f（x）=2，求x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知集合A={x|y=log2（1-x）＜1}，集合B={y|y=2x，x∈A}，则A∩B=（$\frac{1}{2}$，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．函数f（x）=|x2-2x|-a有三个零点，则实数a的值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．若F1，F2是双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的两个焦点，P是双曲线上的点，且|PF1|•|PF2|=32，试求△F1PF2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

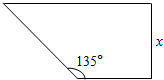    7．某植物园要建形状为直角梯形的苗圃（如图所示），两条邻边借用夹角为135°的两面墙，另两条边的总长为60m，设垂直于底边的腰长为x（m）．
    （1）求苗圃面积S关于边长x的函数解析式S（x）并指出该函数的定义域；
    （2）当x为何值时，面积S最大？最大面积是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．${∫}_{1}^{2}$（x+2x）dx等于（　　）
    A．（x+2x）|${\;}_{1}^{2}$B．（x2+2xln2）|${\;}_{1}^{2}$
    C．（$\frac{{x}^{2}}{2}$+2x）|${\;}_{1}^{2}$D．（$\frac{{x}^{2}}{2}$+$\frac{{2}^{x}}{ln2}$）|${\;}_{1}^{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知数列{an}的前n项和为Sn，Sn≠0，且Sn=a1（an-1）．求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．证明：若f（x）=ax+b，则f（$\frac{{x}_{1}+{x}_{2}}{2}$）=$\frac{f（{x}_{1}）+f（{x}_{2}）}{2}$．

    查看答案和解析>>

    同步练习册答案