
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别是双曲线
的左、右顶点分别是双曲线![]() :
:![]() 的左、右焦点,且
的左、右焦点,且![]() 与
与![]() 相交于点(
相交于点(![]() ).
).
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() 与椭圆
与椭圆![]() 交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
(命题意图)本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率,是简单题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列![]() 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为坐标原点,过点
为坐标原点,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() ,
,![]() ,试探究:
,试探究:![]() 是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
是否为定值.若为定值,求出该定值,若不为定值,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校近几年来通过“书香校园”主题系列活动,倡导学生整本阅读纸质课外书籍.下面的统计图是该校2013年至2018年纸质书人均阅读量的情况,根据统计图提供的信息,下列推断不合理的是( )
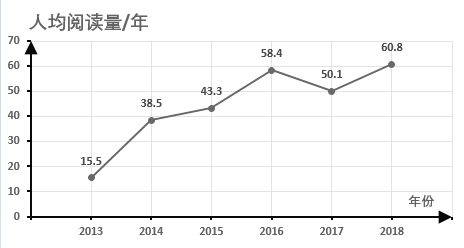
A.从2013年到2016年,该校纸质书人均阅读量逐年增长
B.2013年至2018年,该校纸质书人均阅读量的中位数是46.7本
C.2013年至2018年,该校纸质书人均阅读量的极差是45.3本
D.2013年至2018年,该校后三年纸质书人均阅读量总和是前三年纸质书人均阅读量总和的2倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,右顶点
,右顶点![]() ,上顶点为B,左右焦点分别为
,上顶点为B,左右焦点分别为![]() ,且
,且![]() ,过点A作斜率为
,过点A作斜率为![]() 的直线l交椭圆于点D,交y轴于点E.
的直线l交椭圆于点D,交y轴于点E.
(1)求椭圆C的方程;
(2)设P为![]() 的中点,是否存在定点Q,对于任意的
的中点,是否存在定点Q,对于任意的![]() 都有
都有![]() ?若存在,求出点Q;若不存在,请说明理由.
?若存在,求出点Q;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com