
【题目】某单位建造一间地面面积为12m2的背面靠墙的矩形小房子,由于地理位置的限制,房子侧面的长度x不得超过am.房屋正面的造价为400元/m2 , 房屋侧面的造价为150元/m2 , 屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.当侧面的长度为多少时,总造价最低?
【答案】解:设总造价为Z元,则xy=12,有y= ![]()
∴Z=3y×400+6x×150+5800
=900(x+ ![]() )+5800
)+5800
≥900×2 ![]() +5800
+5800
=13000 …(6分)
当 x= ![]() 时,即x=4时,Z有最小值13000,
时,即x=4时,Z有最小值13000,
若a≥4时,则x=4总进价最低,最低总造价是13000元.
当0<a<4时,则y′=900(1﹣ ![]() )
)
∴当0<x<4时,y′<0,故函数y=900(x+ ![]() )+5800(0,a]上是减函数,
)+5800(0,a]上是减函数,
∴当x=a时,y有最小值,即最低总造价为900(a+ ![]() )+5800元
)+5800元
答:当a≥4时,x=4总造价最低,最低总造价是13000元;
当0<a<4时,x=a总造价最低,最低总造价为900(a+ ![]() )+5800元.
)+5800元.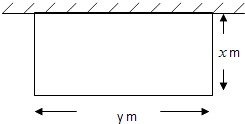
【解析】已知中地面面积为12m2 , 我们可得xy=12有y= ![]() ,根据房屋正面的造价为400元/m2 , 房屋侧面的造价为150元/m2 , 屋顶的造价共5200元,结合墙高为3m,我们可以构造房屋总造价的函数解析式,利用基本不等式或导数即可求出函数的最小值,进而得到答案.
,根据房屋正面的造价为400元/m2 , 房屋侧面的造价为150元/m2 , 屋顶的造价共5200元,结合墙高为3m,我们可以构造房屋总造价的函数解析式,利用基本不等式或导数即可求出函数的最小值,进而得到答案.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】现在的安卓手机盛行一款“心有灵犀”的猜数字游戏,具体的规则如下:
玩家随机输入0~5中的三位数字(数字不重复),按“OK”键确定答案是否正确,手机会给出“xAyB”的提示,其中“xA”表示你输入的三位数字中,有“x”个数字和位置都与答案相同,其中“yB”表示你输入的三位数字中,有“y”个数字与答案相同,但是位置不同,例如:答案为“012”,当你输入“132”时会显示:“1A1B”.
(1)当你第一次输入时,手机显示“1A1B”的概率为多少?
(2)当你第一次输入时,且手机显示“xA2B”时,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:方程x2+mx+1=0有两个不等的实数根,命题q:方程4x2+4(m﹣2)x+1=0无实数根.若p∧q为假,若p∨q为真,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是不在抛物线上的一个动点,过点
是不在抛物线上的一个动点,过点![]() 向抛物线
向抛物线![]() 作两条切线
作两条切线![]() ,切点分别为
,切点分别为![]() .
.
(1)如果点![]() 在直线
在直线![]() 上,求
上,求![]() 的值;
的值;
(2)若点![]() 在以
在以![]() 为圆心,半径为4的圆上,求
为圆心,半径为4的圆上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
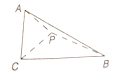
【题目】已知直角三角形![]() 的两条直角边
的两条直角边![]() ,
, ![]() ,
, ![]() 为斜边
为斜边![]() 上一点,沿
上一点,沿![]() 将三角形折成直二面角
将三角形折成直二面角![]() ,此时二面角
,此时二面角![]() 的正切值为
的正切值为![]() ,则翻折后
,则翻折后![]() 的长为( )
的长为( )
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 过点
过点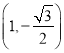 ,记椭圆
,记椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() ,记
,记![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)满足:对任意x∈R,都有f(x+1)+f(x)=2x2﹣2x﹣3
(1)求f(x)的解析式;
(2)若关于x的方程f(x)=a有两个实数根x1 , x2 , 且满足:﹣1<x1<2<x2 , 求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com