
【题目】如图(1)是一直角墙角,![]() ,墙角的两堵墙面和地面两两互相垂直.
,墙角的两堵墙面和地面两两互相垂直.![]() 是一块长
是一块长![]() 为
为![]() 米,宽
米,宽![]() 为
为![]() 米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物.
米的板材,现欲用板材与墙角围成一个直棱柱空间堆放谷物. 
(1)若按如图(1)放置,如何放置板材才能使这个直棱柱空间最大?
(2)由于墙面使用受限,![]() 面只能使用
面只能使用![]() 米,
米,![]() 面只能使用
面只能使用![]() 米.此矩形板材可以折叠围成一个直四棱柱空间,如图(2),如何折叠板材才能使这个空间最大?
米.此矩形板材可以折叠围成一个直四棱柱空间,如图(2),如何折叠板材才能使这个空间最大?
【答案】(1) 板材与墙面![]() 成45°角;(2)见解析.
成45°角;(2)见解析.
【解析】分析:(1)设![]() ,且
,且![]() 因为直三棱柱的高为定值,故底面面积最大时体积最大,利用基本不等式可得
因为直三棱柱的高为定值,故底面面积最大时体积最大,利用基本不等式可得![]() ;(2)因为直四棱柱的高为定值,故底面面积最大时体积最大,又
;(2)因为直四棱柱的高为定值,故底面面积最大时体积最大,又![]() 的面积为定值,只需寻找
的面积为定值,只需寻找![]() 面积的最大值,作
面积的最大值,作![]() 只需
只需![]() 最大即可,设
最大即可,设![]() 则
则![]() ,可得
,可得![]() ,利用二次函数的性质可得结果.
,利用二次函数的性质可得结果.
详解:(1)设![]() ,且
,且![]()
因为直三棱柱的高为定值,故底面面积最大时体积最大
![]()
![]() ,
,
当且仅当![]() 取到等号.
取到等号.
即板材放置时,使得板材与墙面![]() 成45°角.
成45°角.
(2)因为直四棱柱的高为定值,故底面面积最大时体积最大,又![]() 的面积为定值,只需寻找
的面积为定值,只需寻找![]() 面积的最大值.
面积的最大值.
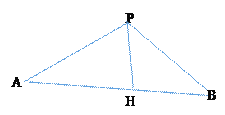 又在
又在![]() 中
中![]() ,只需寻找AB边上高的最大值即可.
,只需寻找AB边上高的最大值即可.
如图:作![]()
设![]() 则
则![]()
![]()
![]()
![]()
当![]() 时PH最大,此时
时PH最大,此时![]()
即板材放置时,沿中间折叠,使得PA=PB.


科目:高中数学 来源: 题型:
【题目】下列说法的错误的是( )
A. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
B. 经过定点![]() 的倾斜角不为
的倾斜角不为![]() 的直线的方程都可以表示为
的直线的方程都可以表示为![]()
C. 不经过原点的直线的方程都可以表示为![]()
D. 经过任意两个不同的点![]() 、
、![]() 直线的方程都可以表示为
直线的方程都可以表示为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验设备M与设备N的生产效率,研究人员作出统计,得到如下表所示的结果,则
设备M | 设备N | |
生产出的合格产品 | 48 | 43 |
生产出的不合格产品 | 2 | 7 |
附:
P(K2≥k0) | 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]() .
.
A. 有90%的把握认为生产的产品质量与设备的选择有关
B. 没有90%的把握认为生产的产品质量与设备的选择有关
C. 可以在犯错误的概率不超过0.01的前提下认为生产的产品质量与设备的选择有关
D. 不能在犯错误的概率不超过0.1的前提下认为生产的产品质量与设备的选择有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列3项抽样调查:
①从15种疫苗中抽取5种检测是否合格.
②涡阳县某中学共有480名教职工,其中一线教师360名,行政人员48名,后勤人员72名.为了解教职工对学校校务公开方面的意见,拟抽取一个容量为20的样本.
③涡阳县某中学报告厅有28排,每排有35个座位,一次报告会恰好坐满了听众,报告会结束后,为了听取意见,需要请28名听众进行座谈.
较为合理的抽样方法是( )
A. ①简单随机抽样, ②系统抽样, ③分层抽样
B. ①简单随机抽样, ②分层抽样, ③系统抽样
C. ①系统抽样, ②简单随机抽样, ③分层抽样
D. ①分层抽样, ②系统抽样, ③简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且 .
.
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入﹣年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列{cn},如果存在常数p、q使得cn+1=pcn+q对任意n∈N*都成立,则称{cn}为“M类数列”.
(1)若{an}是公差为d的等差数列,判断{an}是否为“M类数列”,并说明理由;
(2)若{an}是“M类数列”且满足:a1=2,an+an+1=32n.
①求a2、a3的值及{an}的通项公式;
②设数列{bn}满足:对任意的正整数n,都有a1bn+a2bn﹣1+a3bn﹣2+…+anb1=32n+1﹣4n﹣6,且集合M={n|![]() ≥λ,n∈N*}中有且仅有3个元素,试求实数λ的取值范围.
≥λ,n∈N*}中有且仅有3个元素,试求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com