
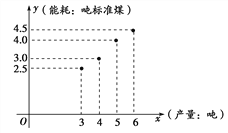
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: 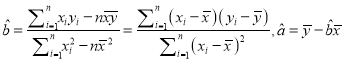 .
.
【答案】(1)答案见解析;(2) ![]() ;(3)19.65.
;(3)19.65.
【解析】试题分析:
(1)结合题中的数据绘制散点图即可;
(2)结合样本中心点求得回归方程可得回归方程为![]() ;
;
(3)结合(2)中求得的回归方程利用其预测作用可预测生产100吨甲产品的生产能耗比技改前降低19.65吨标准煤.
试题解析:
(1)由题意,作散点图如图.
(2)由对照数据,计算得![]() xiyi=66.5,
xiyi=66.5,
![]() x=32+42+52+62=86,
x=32+42+52+62=86,
![]() =4.5,
=4.5,![]() =3.5,
=3.5,
![]() =
=![]() =
=![]() =0.7,
=0.7,
![]() =
=![]() -
-![]()
![]() =3.5-0.7×4.5=0.35,
=3.5-0.7×4.5=0.35,
所以回归方程为![]() =0.7x+0.35
=0.7x+0.35
(3)当x=100时,
y=100×0.7+0.35=70.35(吨标准煤),
预测生产100吨甲产品的生产能耗比技改前降低90-70.35=19.65(吨标准煤)


科目:高中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A.?![]() ∈R,使sin(
∈R,使sin(![]() )=
)=![]() +sinβ
+sinβ
B.?![]() ∈R,函数f(x)=sin(
∈R,函数f(x)=sin(![]() )都不是偶函数
)都不是偶函数
C.?m∈R,使f(x)=(m-1)·m2-4m+3是幂函数,且在(0,+∞)上单调递减
D.?![]() >0,函数f(x)=ln2x+lnx-
>0,函数f(x)=ln2x+lnx-![]() 有零点
有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示讲授概念的时间(单位:min),可有以下的关系:f(x)= 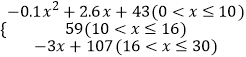
(Ⅰ)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(Ⅱ)开讲后多少min学生的接受能力最强?能维持多少时间?
(Ⅲ)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员400人,每人每年可创利10万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.05万元,但公司需付下岗职员每人每年2万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ![]() ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com