
分析 (1)根据题意f(x)在原点有定义,且为奇函数,从而f(0)=0,这样便可求出b=0,再根据$f(\frac{1}{3})=\frac{3}{10}$即可求出a=1,从而得出f(x)=$\frac{x}{{x}^{2}+1}$;
(2)根据增函数的定义,设任意的x1,x2∈(-1,1),且x1<x2,然后作差,通分,提取公因式x1-x2,证明f(x1)<f(x2),便可得出f(x)在(-1,1)上是增函数;
(3)根据(2)的作差后得到的$f({x}_{1})-f({x}_{2})=\frac{({x}_{1}-{x}_{2})(1-{x}_{1}{x}_{2})}{({{x}_{1}}^{2}+1)({{x}_{2}}^{2}+1)}$,便可看出x1,x2∈(-∞,-1],或x1,x2∈[1,+∞)时,f(x1)>f(x2),从而便得出f(x)的单调递减区间,这样根据f(x)在R上的单调性便可得出f(x)的最小值和最大值.
解答 解:(1)f(x)是定义在(-∞,+∞)上的奇函数;
∴f(0)=0;
即$\frac{0+2015b}{0+1}=0$;
∴b=0;
∴$f(x)=\frac{ax}{{x}^{2}+1}$;
又$f(\frac{1}{3})=\frac{3}{10}$;
∴$\frac{\frac{a}{3}}{\frac{1}{9}+1}=\frac{3}{10}$;
∴a=1;
∴$f(x)=\frac{x}{{x}^{2}+1}$;
(2)证明:设x1,x2∈(-1,1),且x1<x2,则:
$f({x}_{1})-f({x}_{2})=\frac{{x}_{1}}{{{x}_{1}}^{2}+1}-\frac{{x}_{2}}{{{x}_{2}}^{2}+1}$=$\frac{({x}_{1}-{x}_{2})(1-{x}_{1}{x}_{2})}{({{x}_{1}}^{2}+1)({{x}_{2}}^{2}+1)}$;
∵-1<x1<x2<1;
∴x1-x2<0,-1<x1x2<1,1-x1x2>0;
∴f(x1)<f(x2);
∴f(x)在(-1,1)上是增函数;
(3)f(x)的单调减区间为(-∞,-1],[1,+∞);
当x=-1时,f(x)取最小值$-\frac{1}{2}$;当x=1时,f(x)取最大值$\frac{1}{2}$.
点评 考查奇函数在原点有定义时,f(0)=0,已知函数求值的方法,增函数的定义,根据增函数的定义证明一个函数为增函数的方法和过程,作差的方法比较f(x1)与f(x2),作差后为分式的一般要通分,一般提取公因式x1-x2,根据函数单调性求函数最值的方法.


科目:高中数学 来源: 题型:选择题
| A. | f(2014)>f(2015)>f(2016) | B. | f(2016)>f(2014)>f(2015) | ||
| C. | f(2016)=f(2014)>f(2015) | D. | f(2014)>f(2015)=f(2016) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
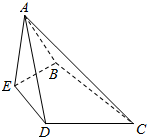 等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).
等边△ABC中,D,E分别是AC,AB的中点,沿DE将△ADE折起,使平面ADE⊥平面BCDE(如图所示).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,-3) | B. | (-2,-$\frac{3}{2}$ ) | C. | (-$\frac{3}{2}$,-1)? | D. | (-1,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,1) | B. | (-1,5) | C. | (-7,2) | D. | (2,-7) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
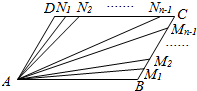 如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )
如图,已知平行四边形ABCD,点M1,M2,M3,…,Mn-1和N1,N2,N3,…,Nn-1分别将线段BC和DCn等分(n∈N*,n≥2),若$\overrightarrow{A{M}_{1}}$$+\overrightarrow{A{M}_{2}}$+…$+\overrightarrow{A{M}_{n-1}}$+$\overrightarrow{A{N}_{1}}$$+\overrightarrow{A{N}_{2}}$+…$+\overrightarrow{A{N}_{n-1}}$=30$\overrightarrow{AC}$,则n=( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com