
设 是函数
是函数
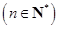 的零点.
的零点.
(1)证明: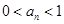 ;
;
(2)证明:
 .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)借助导数证明函数 在
在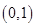 是单调函数,进而确定函数
是单调函数,进而确定函数 在
在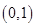 上有且只有一个零点,进而证明
上有且只有一个零点,进而证明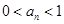 ;(2)先将原不等式化为两个不等式
;(2)先将原不等式化为两个不等式 与
与 ,先证明不等式
,先证明不等式 ,方法1先证明不等式
,方法1先证明不等式 ,然后利用放缩法证明
,然后利用放缩法证明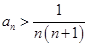 ,从而证明不等式
,从而证明不等式 成立,方法2是在不等式
成立,方法2是在不等式 的基础上利用数学归纳法直接证明不等式
的基础上利用数学归纳法直接证明不等式 成立;再证明不等式
成立;再证明不等式
先考察函数 的单调性证明
的单调性证明 ,然后就
,然后就 时,将对
时,将对 进行放缩,
进行放缩, ,进而证明
,进而证明 。
。
试题解析:(1)因为 ,
,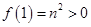 ,且
,且 在
在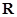 上的图像是一条连续曲线,
上的图像是一条连续曲线,
所以函数 在
在 内有零点. 1分
内有零点. 1分
因为 ,
,
所以函数 在
在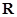 上单调递增. 2分
上单调递增. 2分
所以函数 在
在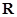 上只有一个零点,且零点在区间
上只有一个零点,且零点在区间 内.
内.
而 是函数
是函数 的零点,
的零点,
所以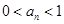 . 3分
. 3分
(2)先证明左边的不等式:
因为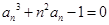 ,
,
由(1)知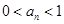 ,
,
所以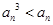 . 4分
. 4分
即 .
.
所以 . 5分
. 5分
所以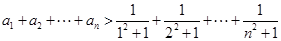 . 6分
. 6分
以下证明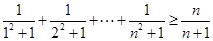 . ①
. ①
方法1(放缩法):因为 , 7分
, 7分
所以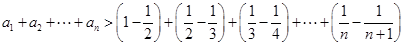
 . 9分
. 9分
方法2(数学归纳法):1)当 时,
时,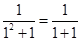 ,不等式①成立.
,不等式①成立.
2)假设当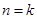 (
( )时不等式①成立,即
)时不等式①成立,即 .
.
那么
 .
.
以下证明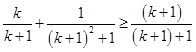 . ②
. ②
即证


科目:高中数学 来源: 题型:解答题
观察下表:
1,
2,3
4,5,6,7
8,9,10,11,12,13,14,15,
…
问:(1)此表第n行的最后一个数是多少?
(2)此表第n行的各个数之和是多少?
(3)2 008是第几行的第几个数?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin 13°cos 17°;
②sin215°+cos215°-sin 15°cos 15°;
③sin218°+cos212°-sin 18°cos 12°;
④sin2(-18°)+cos248°-sin(-18°)cos 48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos 55°.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com