
有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下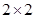 联表:
联表:
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合计 | | | 200 |
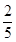
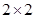 联表;
联表;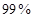 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系” ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望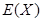 和方差
和方差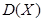

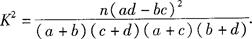
(1)
(2) 优秀 非优秀 合计 甲班 30 70 100 乙班 50 50 100 合计 80 120 200 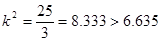 ,有
,有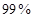 的把握
的把握
(3)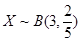 ,
,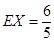 ,
,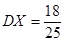
解析试题分析:(1)根据题意,由于全部200人中随机抽取1人为优秀的概率为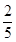 ,那么可知优秀的人数为80,那么可知不优秀的人数为120,那么可知得到列联表为:
,那么可知优秀的人数为80,那么可知不优秀的人数为120,那么可知得到列联表为:
(2)根据a=30,b=70,c=50,d=120,结合公式 优秀 非优秀 合计 甲班 30 70 100 乙班 50 50 100 合计 80 120 200 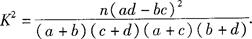 ,可知
,可知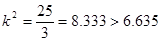 ,有
,有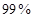 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系”
(3)由于全部200人中有放回抽取3次,每次抽取一人,记被抽取的3人中优秀的人数为 ,那么可知
,那么可知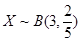 ,
,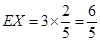 ,
,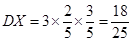 ,。
,。
考点:列联表和独立性检验
点评:主要是考查了独立性检验的思想的运用,以及二项分布的运用,属于中档题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
2012年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类: 第一类的用电区间在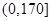 ,第二类在
,第二类在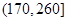 ,第三类在
,第三类在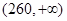 (单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
(单位:千瓦时). 某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
⑴ 求该小区居民用电量的中位数与平均数;
⑵ 本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;
⑶ 利用分层抽样的方法从该小区内选出5户居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率. 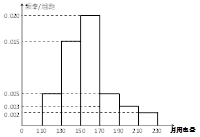
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了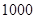 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.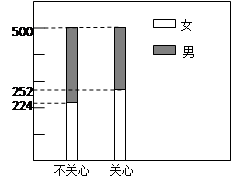
(1)完成列联表,并判断能否有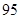 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
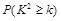 | 0.10 | 0.05 | 0.01 |
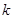 | 2.706 | 3.841 | 6.635 |
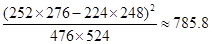
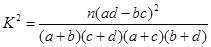 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望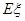 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查某地区大学生是否爱好某项体育运动,用简单随机抽样方法从该地区的大学里调查了500位大学生,结果如下:
| | 男 | 女 |
| 爱好 | 40 | 30 |
| 不爱好 | 160 | 270 |
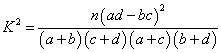
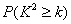 | 0.050 | 0.010 | 0.001 |
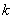 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(t)与相应的生产能耗y(t标准煤)的几组对照数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某大学体育学院在2012年新招的大一学生中,随机抽取了 40名男生,他们的身高(单位:cm)情况共分成五组:第1组[175,180),第 2 组[180,185),第 3 组 [185,190),第 4 组[190,195),第 5 组[195,200) .得到的频率分布直方图(局部)如图所示,同时规定身高在185cm以上(含185cm)的学生成为组建该校篮球队的“预备生”.
(I)求第四组的频率并补布直方图;
(II)如果用分层抽样的方法从“预备生”和“非预备生”中选出5人,再从这5人中随机选2人,那么至少有1人是“预备生”的概率是多少?
(III)若该校决定在第4,5组中随机抽取2名学生接受技能测试,第5组中有ζ名学生接受测试,试求ζ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com