
| A. | a=0 | B. | a≥$\frac{9}{8}$ | C. | a=0或a≥$\frac{9}{8}$ | D. | 不确定 |
分析 因集合A是方程ax2-3x+2=0的解集,欲使集合A={x|ax2-3x+2=0}至多有一个元素,只须此方程有两个相等的实数根或没有实数根,或只有一个实根,下面对a进行讨论求解即可.
解答 解:∵集合A={x|ax2-3x+2=0}至多有一个元素,
分类讨论:
①当a=0时,A={x|-3x+2=0}只有一个元素,符合题意;
②当a≠0时,要A={x|ax2-3x+2=0}至多有一个元素,
则必须方程:ax2-3x+2=0有两个相等的实数根或没有实数根,
∴△≤0,得:9-8a≤0,∴a≥$\frac{9}{8}$,
故选:C.
点评 本小题主要元素与集合关系的判断、不等式的解法等基础知识,考查运算求解能力,考查分类讨论、化归与转化思想.属于基础题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$<$\frac{f(1)}{f(2)}$<$\frac{1}{8}$ | B. | $\frac{1}{8}$<$\frac{f(1)}{f(2)}$<$\frac{1}{4}$ | C. | $\frac{1}{4}$<$\frac{f(1)}{f(2)}$<$\frac{1}{3}$ | D. | $\frac{1}{3}$<$\frac{f(1)}{f(2)}$<$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
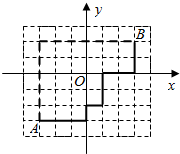 现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{5}{6}$ | C. | -$\frac{7}{18}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com