
 );
); 2,b=
2,b= 3,c=(
3,c=( )0.5大小关系是a>b>c.
)0.5大小关系是a>b>c.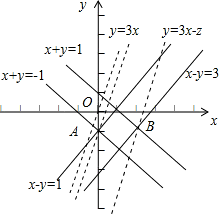
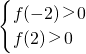 ,解得
,解得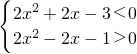 ,即
,即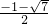 <x<
<x<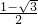 ,故②错误;
,故②错误; +3,
+3,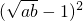 ≥4,
≥4, -1≤-2(舍),或
-1≤-2(舍),或 -1≥2,
-1≥2,

科目:高中数学 来源: 题型:
| n |
| M |
| AM |
| n |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+2x-3 |
查看答案和解析>>
科目:高中数学 来源:2014届河北省衡水市高二9月月考数学试卷(解析版) 题型:选择题
下列命题正确的个数为 ( )
①已知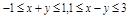 ,则
,则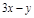 的范围是
的范围是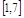 ;
;
②若不等式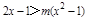 对满足
对满足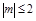 的所有m都成立,则x的范围是
的所有m都成立,则x的范围是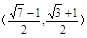 ;
;
③如果正数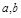 满足
满足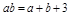 ,则
,则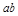 的取值范围是
的取值范围是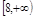
④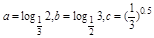 大小关系是
大小关系是
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2009-10学年黑龙江佳一中高一第三学段考试数学 题型:选择题
在空间中,下列命题正确的个数为( )
(1)有两组对边相等的四边形是平行四边形 (2)四边相等的四边形是菱形
(3)平行于同一条直线的两条直线平行 (4)有两边及其夹角对应相等的两个三角形全等
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com