
【题目】如图所示,在直三棱柱![]() 中,
中, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证: ![]() ∥平面
∥平面![]() ;
;
(2)若![]() ,求证:
,求证: ![]() .
.

科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中曲线![]() 的方程是
的方程是![]() ,点
,点![]() 是
是![]() 上的动点,点
上的动点,点![]() 满足
满足![]() (
(![]() 为极点),点
为极点),点![]() 的轨迹为曲线
的轨迹为曲线![]() ,以极点
,以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系
轴的非负半轴建立平面直角坐标系![]() ,已知直线
,已知直线![]() 的参数方程是
的参数方程是![]() ,(
,( ![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 直角坐标方程与直线
直角坐标方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市初三毕业生参加中考要进行体育测试,某实验中学初三(8)班的一次体育测试成绩的茎叶图和频率分布直方图都受到不同程度的涂黑,但可见部分如图,据此解答如下问题.
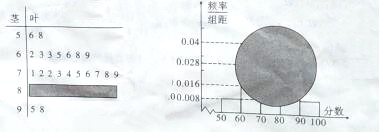
(Ⅰ)求全班人数及中位数,并重新画出频率直方图;
(Ⅱ)若要从分数在![]() 之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在
之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 满足
满足![]() ,其中
,其中![]() ,且
,且![]() ,
, ![]() 为常数.
为常数.
(1)若![]() 是等差数列,且公差
是等差数列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且存在
,且存在![]() ,使得
,使得![]() 对任意的
对任意的![]() 都成立,求
都成立,求![]() 的最小值;
的最小值;
(3)若![]() ,且数列
,且数列![]() 不是常数列,如果存在正整数
不是常数列,如果存在正整数![]() ,使得
,使得![]() 对任意的
对任意的![]() 均成立. 求所有满足条件的数列
均成立. 求所有满足条件的数列![]() 中
中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A, B, C的对边分别为a, b, c,且![]() .
.
(Ⅰ)求角C的大小;
(Ⅱ)设角A的平分线交BC于D,且AD=![]() ,若b=
,若b=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届山西省太原十二中高三上学期1月月考】运动员甲在最近![]() 场
场![]() 比赛中所得分数的茎叶图如图所示,由于疏忽,茎叶图中的两个数据上出行了污渍,导致这两个数字无法辨认,但统计员记得除掉污渍
比赛中所得分数的茎叶图如图所示,由于疏忽,茎叶图中的两个数据上出行了污渍,导致这两个数字无法辨认,但统计员记得除掉污渍![]() 处的数字不影响整体中位数,且这六个数据的平均值为
处的数字不影响整体中位数,且这六个数据的平均值为![]() .
.
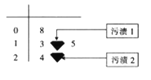
(1)求污渍![]() 处的数字;
处的数字;
(2)篮球运动员乙在最近![]() 场
场![]() 的比赛中所得分数为
的比赛中所得分数为![]() .试分别以各自
.试分别以各自![]() 场比赛得分的平均数与方差来分析这两名篮球运动员的发挥水平.
场比赛得分的平均数与方差来分析这两名篮球运动员的发挥水平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com