
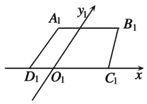
 如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )
如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若AD∥Oy,AB∥CD,A1B1=$\frac{3}{4}{C_1}{D_1}=3,{A_1}{D_1}$=1,则原平面图形ABCD的面积是( )| A. | 14. | B. | 7 | C. | $14\sqrt{2}$ | D. | $7\sqrt{2}$ |
分析 如图,根据直观图画法的规则,确定原平面图形四边形ABCD的形状,求出底边边长,上底边边长,以及高,然后求出面积.
解答 解:如图,根据直观图画法的规则,
直观图中A1D1∥O′y′,A1D1=1,⇒原图中AD∥Oy,
从而得出AD⊥DC,且AD=2A1D1=2,
直观图中A1B1∥C1D1,A1B1=$\frac{3}{4}$C1D1=3,⇒原图中AB∥CD,AB=$\frac{3}{4}$CD=3,
即四边形ABCD上底和下底边长分别为3,4,高为2,如图.
故其面积S=$\frac{1}{2}$(3+4)×2=7.
故选:B.
点评 本题考查平面图形的直观图,考查计算能力,作图能力,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9600}$ | B. | $\frac{1}{18000}$ | C. | $\frac{1}{4500}$ | D. | $\frac{1}{10800}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在${x_0}∈R,{2^{x_0}}>0$ | B. | ?x∈R,2x>0 | ||
| C. | $?{x_0}∈R,{2^{x_0}}≥0$. | D. | ?x∈R,2x≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 图象向右平移$\frac{π}{3}$个单位长度得到y=sin2x图象 | |
| B. | 图象关于点($\frac{π}{6}$,0)对称 | |
| C. | 图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 在区间[-$\frac{5π}{12}$,$\frac{π}{12}$]单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2018,-2016) | B. | (-∞,-2016) | C. | (-2019,-2016) | D. | (-∞,-2019) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com