已知数列{an}满足:a1=1,a2=4,且对任意的n≥3,n∈N*有an-4an-1+4an-2=0.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)是否存在等差数列{bn},使得对任意的n∈N*有an=b1Cn1+b2Cn2+…+bnCnn成立?证明你的结论.
解:(Ⅰ)∵a
n-4a
n-1+4a
n-2=0,
∴a
n-2a
n-1=2(a
n-1-2a
n-2)(其中n≥3);
∴

=2,(其中n≥3);
∴数列{a
n-2a
n-1}是首项为(a
2-2a
1),公比为2的等比数列,
∵a
2-2a
1=2,∴a
n-2a
n-1=2•2
n-2=2
n-1(其中n≥2);
∴
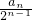
-
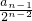
=1,∴数列{
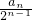
}是首项为1,公差为1的等差数列,故
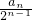
=n,即a
n=n•2
n-1;
(Ⅱ)令n=1,2,3,代入a
n=b
1C
n1+b
2C
n2+…+b
nC
nn得:
b
1=1①,b
1C
21+b
2C
22=4②,b
1C
31+b
2C
32+b
3C
33=12③;
由①②③组成方程组,解得:b
1=1,b
2=2,b
3=3;
由此可猜想b
n=n,即n•2
n-1=C
n1+2C
n2+…+nC
nn下面用数学归纳法证明:
(1)当n=1时,等式左边=1,右边=C
11=1,
∴当n=1时,等式成立,
(2)假设当n=k时,等式成立,即k•2
k-1=C
k1+2C
k2+…+kC
kk当n=k+1时
(k+1)•2
k+1-1=k•2
k+2
k=2k•2
k-1+2
k=2(C
k1+2C
k2+…+kC
kk)+(C
k0+C
k1+…+C
kk)
=2C
k1+4C
k2+…+2kC
kk+C
k0+C
k1+…+C
kk=(C
k0+C
k1)+2(C
k1+C
k2)+3(C
k2+C
k3)+…+(k+1)C
kk=C
k+11+2C
k+12+3C
k+13+…+(k+1)C
k+1k+1∴当n=k+1时,等式成立,
综上所述,存在等差数列b
n=n,使得对任意的n∈N
*有a
n=b
1C
n1+b
2C
n2+…+b
nC
nn成立.
分析:(Ⅰ)由a
n-4a
n-1+4a
n-2=0,得a
n-2a
n-1=2(a
n-1-2a
n-2)(其中n≥3);即

=2,得数列{a
n-2a
n-1}是等比数列;首项a
2-2a
1=2,则通项a
n-2a
n-1=2•2
n-2=2
n-1(其中n≥2);从而得数列a
n的通项公式;
(Ⅱ)当n=1,2,3时,由a
n=b
1C
n1+b
2C
n2+…+b
nC
nn得:b
1=1①,b
1C
21+b
2C
22=4②,b
1C
31+b
2C
32+b
3C
33=12③;由①②③组成方程组,得b
1,b
2,b
3;由此猜想b
n的通项公式,即n•2
n-1=C
n1+2C
n2+…+nC
nn;用数学归纳法证明即可.
点评:本题综合考查了数列与递推公式的应用,组合数公式与数学归纳法的应用;解题时应细心分析,认真解答,以免出错.

 =2,(其中n≥3);
=2,(其中n≥3);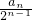 -
-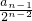 =1,∴数列{
=1,∴数列{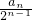 }是首项为1,公差为1的等差数列,故
}是首项为1,公差为1的等差数列,故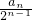 =n,即an=n•2n-1;
=n,即an=n•2n-1; =2,得数列{an-2an-1}是等比数列;首项a2-2a1=2,则通项an-2an-1=2•2n-2=2n-1(其中n≥2);从而得数列an的通项公式;
=2,得数列{an-2an-1}是等比数列;首项a2-2a1=2,则通项an-2an-1=2•2n-2=2n-1(其中n≥2);从而得数列an的通项公式;

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案