练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知点（m，n）在直线xcosθ+ysinθ=2上，则m2+n2的最小值为
     
    ．
    分析：m2+n2 表示直线上的点（m，n）与原点之间距离的平方，故m2+n2的最小值为原点到直线xcosθ+ysinθ=2的距离的平方，
    由点到直线的距离公式求得原点到直线xcosθ+ysinθ=2的距离的平方．
    解答：解：∵点（m，n）在直线xcosθ+ysinθ=2上，
    ∴m2+n2 表示直线上的点（m，n）与原点之间距离的平方，
    故m2+n2的最小值为原点到直线xcosθ+ysinθ=2的距离的平方，
    故m2+n2的最小值为 (
    |0+0-2|
    		cos2θ+sin2θ
    )    2    =4，
    故答案为 4．
    点评：本题考查点到直线的距离公式的应用，关键是要明确m2+n2所代表的意义，直线上的点（m，n）与原点之间距离最小值就是
    原点到直线的距离．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：天利38套《2008全国各省市高考模拟试题汇编　精华大字版》、数学理 题型：022

    已知l、m、n是直线，α、β是平面，给出命题：

    ①若m∥α，n∥α，则m∥n；

    ②设α－l－β是直二面角，若m⊥l，则m⊥β；

    ③若m、n在α内的射影依次为一个点和一条直线，且m⊥n，则n?α或n∥α；

    ④设m、n是异面直线，若m∥α，则n与α相交．

    其中真命题的序号是________．(把所有真命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源：天利38套《2008全国各省市高考模拟试题汇编　精华大字版》、数学文 精华大字版 题型：022

    已知l、m、n是直线，α、β是平面，给出命题：

    ①若m∥α，n∥α，则m∥n；

    ②设α－l－β是直二面角，若m⊥l，则m⊥β；

    ③若m、n在α内的射影依次为一个点和一条直线，且m⊥n，则或n∥α；

    ④设m、n是异面直线，若m∥α，则n与α相交．

    其中真命题的序号是________．(把所有真命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知l、m、n是直线，α、β是平面，给出命题：

    ①若m∥α，n∥α，则m∥n；

    ②设α-l-β是直二面角，若m⊥l，则m⊥β；

    ③若m、n在α内的射影依次为一个点和一条直线，且m⊥n，则nα或n∥α；

    ④设m、n是异面直线，若m∥α，则n与α相交.

    其中真命题的序号是___________(把所有真命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知l、m、n是直线，α、β是平面，给出命题：

    ①若m∥α，n∥α，则m∥n；

    ②设α-l-β是直二面角，若m⊥l，则m⊥β；

    ③若m、n在α内的射影依次为一个点和一条直线，m⊥n，则nα或n∥α；

    ④设m、n是异面直线，若m∥α，则n与α相交．

    其中真命题的序号是___________.(把所有真命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

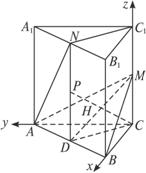
    如图,已知直三棱柱ABC—A1B1C1的底面是以∠C为直角的等腰直角三角形,AC=BC=CC1=2,M、N分别在棱CC1、A1B1上,N是A1B1的中点.

    (1)若M是CC1的中点,求异面直线AN与BM所成的角;

    (2)若点C关于平面ABM的对称点恰好在平面ABB1A1上,试确定M点在CC1上的位置.

    查看答案和解析>>

    同步练习册答案