
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)求证:当![]() 时,
时, ![]() ;
;
(Ⅱ)若函数![]() 在(1,+∞)上有唯一零点,求实数
在(1,+∞)上有唯一零点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)(0,1)
【解析】试题分析:(Ⅰ)求导![]() ,得
,得![]() ,分析单调性得当
,分析单调性得当![]() 时,
时, ![]() 即得证;(Ⅱ)
即得证;(Ⅱ) ![]() 对t进行讨论①
对t进行讨论①![]() ,
, ![]() 在[1,+∞)上是增函数,所以当
在[1,+∞)上是增函数,所以当![]() 时,
时, ![]() ,所以
,所以![]() 在(1,+∞)上没有零点,②若
在(1,+∞)上没有零点,②若![]() ,
, ![]() 在[1,+∞)上是减函数,所以当
在[1,+∞)上是减函数,所以当![]() 时,
时, ![]() ,所以
,所以![]() 在(1,+∞)上没有零点,③若0<t<1时分析单调性借助于第一问,找到
在(1,+∞)上没有零点,③若0<t<1时分析单调性借助于第一问,找到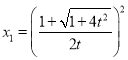 ,则当
,则当![]() 时
时![]() ,即
,即![]() 成立;取
成立;取![]() ,则当
,则当![]() 时,
时, ![]() ,即
,即![]() ,说明存在
,说明存在![]() ,使得
,使得![]() ,即存在唯一零点;
,即存在唯一零点;
试题解析:(Ⅰ)由![]() ,得
,得![]() .
.
当![]() 变化时,
变化时, ![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
x | (0,4) | 4 | (4,+∞) |
| + | 0 | - |
|
|
|
所以当![]() 时,
时, ![]() ;
;
(Ⅱ)![]()
①若![]() ,则当
,则当![]() 时,
时, ![]() ,所以
,所以![]() 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,
所以当![]() 时,
时, ![]() ,所以
,所以![]() 在(1,+∞)上没有零点,所以
在(1,+∞)上没有零点,所以![]() 不满足条件.
不满足条件.
②若![]() ,则当
,则当![]() 时,
时, ![]() ,所以
,所以![]() 在[1,+∞)上是减函数,
在[1,+∞)上是减函数,
所以当![]() 时,
时, ![]() ,所以
,所以![]() 在(1,+∞)上没有零点,所以
在(1,+∞)上没有零点,所以![]() 不满足条件.
不满足条件.
③若0<t<1,则由![]() ,得
,得![]()
当![]() 变化时,
变化时, ![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:

记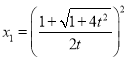 ,则当
,则当![]() 时
时![]() ,即
,即![]() 成立;
成立;
由(Ⅰ)知当![]() 时,
时, ![]() ,即
,即![]() 成立,所以取
成立,所以取![]() ,则当
,则当![]() 时,
时, ![]() 且
且![]() ,从而
,从而![]()
![]() ,即
,即![]() ,这说明存在
,这说明存在![]() ,使得
,使得![]() ,
,
结合上表可知此时函数![]() 在(1,+∞)上有唯一零点,所以0<t<1满足条件.
在(1,+∞)上有唯一零点,所以0<t<1满足条件.
综上,实数![]() 的取值范围为(0,1).
的取值范围为(0,1).


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)
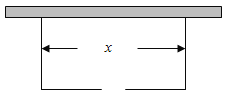
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
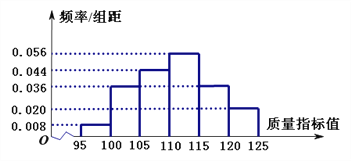
(Ⅰ)将频率视为概率. 若乙套设备生产了5000件产品,则其中的不合格品约有多少件;
(Ⅱ)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(Ⅲ)根据表1和图1,对两套设备的优劣进行比较.
附:

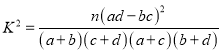 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为![]() ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为![]() ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为![]() 的菱形(边长为
的菱形(边长为![]() ),圆锥的体积为
),圆锥的体积为![]() ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点.在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE.求直线BC与平面ABF所成角的大小,并求线段PH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=![]() ,n=
,n=![]() ,现有如下命题:
,现有如下命题:
①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中真命题有___________________(写出所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com