
【题目】双“十一”结束之后,某网站针对购物情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定:购物600(含600元)以下者,称为“理智购物”,购物超过600元者被网友形象的称为“剁手党”,得到如下统计表:
分组编号 | 年龄分组 | 球迷 | 所占比例 |
1 | [20,25) | 1000 | 0.5 |
2 | [25,30) | 1800 | 0.6 |
3 | [30,35) | 1200 | 0.5 |
4 | [35,40) | a | 0.4 |
5 | [40,45) | 300 | 0.2 |
6 | [45,50] | 200 | 0.1 |
若参与调查的“理智购物”总人数为7720人.
(1)求a的值;
(2)从年龄在[20,35)的“剁手党”中按照年龄区间分层抽样的方法抽取20人; ①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率;
②从这20人中随机抽取2人,用ζ表示年龄在[20,25)之间的人数,求ξ的分布列及期望值.
【答案】
(1)解:由“理智购物”者总人数为7720人,
可得:1000+1800× ![]() +1200+a×
+1200+a× ![]() +300×
+300× ![]() +200×
+200× ![]() =7720,
=7720,
解得a=880
(2)解:①年龄在[20,35)的“剁手党”共有1000+1800+1200=4000人,
则年龄在区间[20,25)的应该抽取5人,年龄在区间[25,30)的应该抽取9人,年龄在区间[30,35)的应该抽取6人.
从这20人中随机抽取2人,这2人属于同一年龄区间的概率为:
P= ![]() =
= ![]() .
.
②由题意可知ξ的取值可能为0,1,2.
P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
故ξ的分布列为:
ξ | 0 | 1 | 2 |
P |
|
|
|
E(ξ)= ![]() =
= ![]()
【解析】(1)由“理智购物”者总人数为7720人,结合题意列出方程,由此能求出a的值.(2)①年龄在[20,35)的“剁手党”有4000人,则年龄在区间[20,25)的应该抽取5人,年龄在区间[25,30)的应该抽取9人,年龄在区间[30,35)的应该抽取6人,由此能求出从这20人中随机抽取2人,这2人属于同一年龄区间的概率.②由题意可知ξ的取值可能为0,1,2.分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
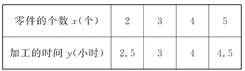
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
,且当n≥2时,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)证明: ![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,
, ![]() 为实数,
为实数, ![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() .
.
(1)当![]() ,
, ![]() 时,设函数
时,设函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最大值;
的最大值;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同实数解,求
上有两个不同实数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
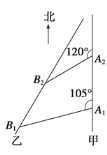
【题目】如图所示,甲船以每小时30![]() 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10![]() 海里.问:乙船每小时航行多少海里?
海里.问:乙船每小时航行多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园![]() ,公园由长方形的休闲区
,公园由长方形的休闲区![]() (阴影部分)和环公园人行道组成.已知休闲区
(阴影部分)和环公园人行道组成.已知休闲区![]() 的面积为4000平方米,人行道的宽分别为4米和10米.
的面积为4000平方米,人行道的宽分别为4米和10米.
(1)若设休闲区的长![]() 米,求公园
米,求公园![]() 所占面积
所占面积![]() 关于
关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区![]() 的长和宽该如何设计?
的长和宽该如何设计?

查看答案和解析>>
科目:高中数学 来源: 题型:
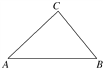
【题目】如图,在△ABC中,已知|AB|=4 ![]() ,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
,且三内角A,B,C满足2sin A+sin C=2sin B,建立适当的坐标系,求顶点C的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点是原点,以
的顶点是原点,以![]() 轴为对称轴,且经过点
轴为对称轴,且经过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() ,
, ![]() .求直线
.求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com