
【题目】已知函数![]() .
.
(1)当![]() ,且
,且![]() 是
是![]() 上的增函数,求实数
上的增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() ,且对任意实数
,且对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 总有三个不相等的实数根,求实数
总有三个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() .
.
⑴ 求证:数列![]() 为等差数列;
为等差数列;
⑵ 设![]() ,
, ![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若当
,若当![]() 且
且![]() 为偶数时,
为偶数时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 设数列![]() 的前
的前![]() 项的和为
项的和为![]() ,试求数列
,试求数列![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设原信息为![]() ,传输信息为
,传输信息为![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 运算规则为:
运算规则为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .例如:原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息出错的是( )
.例如:原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息出错的是( )
A. 01100 B. 11010 C. 10110 D. 11000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )
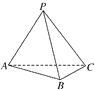
A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
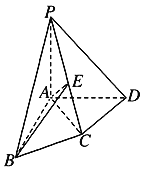
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新鲜的荔枝很好吃,但摘下后容易变黑,影响卖相.某大型超市进行扶贫工作,按计划每年六月从精准扶贫户中订购荔枝,每天进货量相同且每公斤20元,售价为每公斤24元,未售完的荔枝降价处理,以每公斤16元的价格当天全部处理完.根据往年情况,每天需求量与当天平均气温有关.如果平均气温不低于25摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温低于15摄氏度,需求量为
公斤;如果平均气温低于15摄氏度,需求量为![]() 公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
平均气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(Ⅰ)假设该商场在这90天内每天进货100公斤,求这90天荔枝每天为该商场带来的平均利润(结果取整数);
(Ⅱ)若该商场每天进货量为200公斤,以这90天记录的各需求量的频率作为各需求量发生的概率,求当天该商场不亏损的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com