|
|
|
已知某地区中小学学生人数和近视情况分别如图1和如图2所示,为了解该地区中下学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为
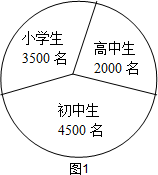
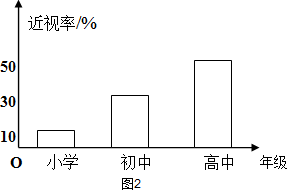
|
| [ ] |
A. |
100,10
|
B. |
200,10
|
C. |
100,20
|
D. |
200,20
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设向量a,b满足|a+b|=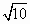 ,|a-b|= ,|a-b|=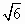 ,则a·b= ,则a·b=
|
| [ ] |
A. |
1
|
B. |
2
|
C. |
3
|
D. |
5
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立.
(Ⅰ)求同一工作日至少3人需使用设备的概率;
(Ⅱ)X表示同一工作日需使用设备的人数,求X的数学期望.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,在平行四边形ABCD中,点E在AB上且EB=2AE,AC与DE交于点F,则 =________. =________.
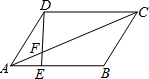
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知集合M={-1,0,1},N={0,1,2},则M∪N=
|
| [ ] |
A. |
{-1,0,1}
|
B. |
{-1,0,1,2}
|
C. |
{-1,0,2}
|
D. |
{0,1}
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
从0,1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的中位数是6的概率为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
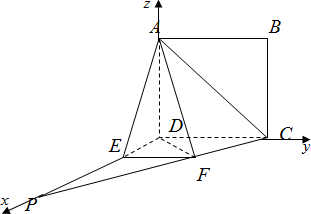
(1)证明:CF⊥平面ADF.
(2)求二面角D-AF-E的余弦值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在△ABC中,A=60°,AC=2,BC= ,则AB等于________. ,则AB等于________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设双曲线C的两个焦点为 , , ,一个顶点式(1,0),则C的方程为 ,一个顶点式(1,0),则C的方程为
________.
|
|
|
查看答案和解析>>
