
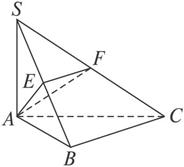
思路解析:本题所给的已知条件中,垂直关系较多,不容易确定如何在证明中使用它们,因而用综合法比较困难.这时,可以从结论出发,逐步反推,寻求使当前命题成立的充分条件.在立体几何中,通常可以把证明两条直线互相垂直的问题转化为证明直线与平面垂直的问题.
证明:要证AF⊥SC,只需证SC⊥平面AEF,只需证AE⊥SC(因为EF⊥SC),只需证AE⊥平面SBC,只需证AE⊥BC(因为AE⊥SB),只需证BC⊥平面SAB,只需证BC⊥SA(因为AB⊥BC).
由SA⊥平面ABC可知,上式成立.
所以AF⊥SC.
方法归纳 注意此处空半格在分析法证明中,从结论出发的每一个步骤所得到的判断都是结论成立的充分条件,最后一步归结到已被证明了的事实.因此,从最后一步可以倒推回去,直到结论,但这个倒推过程可以省略.


科目:高中数学 来源: 题型:
 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:查看答案和解析>>
科目:高中数学 来源: 题型:022
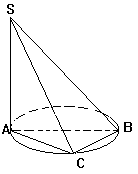
如图, SA垂直于以AB为直径的圆所在的平面, 且∠SBA=30°, C为弧AB 上一点, ∠BAC=α,二面角A-SB-C的平面角为β,则 tanα·tanβ=___________.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
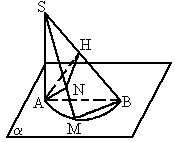
如图,平面a内有一个半圆,直径为AB,过A作SA⊥平面a,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.这个图形中有多少对垂直的直线?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
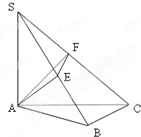
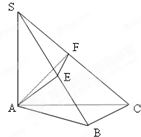 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com