
【题目】【2017福建三明5月质检】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知集合A,B满足,集合A={x|x=7k+3,k∈N},B={x|x=7k﹣4,k∈Z},则A,B两个集合的关系:AB(横线上填入,或=)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知U={1,2,3,4,5,6,7,8},A={1,3,5,7},B={2,4,5}则U(A∪B)( )
A.{6,8}
B.{5,7}
C.{4,6,7}
D.{1,3,5,6,8}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017江西4月质检】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
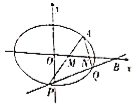
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且斜率大于0的直线
且斜率大于0的直线![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() ,
,![]() ,直线
,直线![]() ,
,![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y. 
(1)写出y关于x的函数关系式,并指出这个函数的定义域.
(2)当AE为何值时,绿地面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017广东佛山二模】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为![]() 、
、![]() 、
、![]() 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).


(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度υ(千米/小时)之间的函数关系为:y= ![]() (υ>0).
(υ>0).
(1)在该时段内,当汽车的平均速度υ为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017四川资阳4月模拟】共享单车是指由企业在校园、公交站点、商业区、公共服务区等场所提供的自行车单车共享服务,由于其依托“互联网+”,符合“低碳出行”的理念,已越来越多地引起了人们的关注.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),…,[90,100]分成5组,制成如图所示频率分直方图.
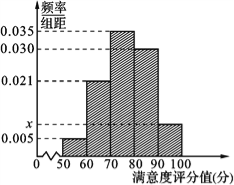
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)已知满意度评分值在[90,100]内的男生数与女生数的比为2:1,若在满意度评分值为[90,100]的人中随机抽取4人进行座谈,设其中的女生人数为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列
(1)在等差数列{an}中,a6=10,S5=5,求该数列的第8项a8;
(2)在等比数列{bn}中,b1+b3=10,b4+b6= ![]() ,求该数列的前5项和S5 .
,求该数列的前5项和S5 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com