
【题目】给定数列![]() ,若满足
,若满足![]() 且
且![]() ,对于任意的n,
,对于任意的n,![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“指数型数列”.
为“指数型数列”.
![]() Ⅰ
Ⅰ![]() 已知数列
已知数列![]() ,
,![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() ,
,![]() 是不是“指数型数列”;
是不是“指数型数列”;
![]() Ⅱ
Ⅱ![]() 若数列
若数列![]() 满足:
满足:![]() ,
,![]() ,判断数列
,判断数列![]() 是否为“指数型数列”,若是给出证明,若不是说明理由;
是否为“指数型数列”,若是给出证明,若不是说明理由;
![]() Ⅲ
Ⅲ![]() 若数列
若数列![]() 是“指数型数列”,且
是“指数型数列”,且![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
【答案】(Ⅰ)![]() 不是指数型数列,
不是指数型数列,![]() 是指数型数列;(Ⅱ)数列
是指数型数列;(Ⅱ)数列![]() 是“指数型数列”;(Ⅲ)详见解析.
是“指数型数列”;(Ⅲ)详见解析.
【解析】
![]() Ⅰ
Ⅰ![]() 利用指数型数列的定义,判断即可;
利用指数型数列的定义,判断即可;![]() Ⅱ
Ⅱ![]() 利用
利用![]() ,
,![]() ,说明数列
,说明数列![]() 是等比数列,然后证明数列
是等比数列,然后证明数列![]() 为“指数型数列”;
为“指数型数列”;![]() Ⅲ
Ⅲ![]() 利用反证法,结合n为偶数以及奇数进行证明即可.
利用反证法,结合n为偶数以及奇数进行证明即可.
![]() Ⅰ
Ⅰ![]() 解:对于数列
解:对于数列![]() ,
,![]() ,
,
所以![]() 不是指数型数列.
不是指数型数列.
对于数列![]() ,对任意n,
,对任意n,![]() ,因为
,因为![]() ,
,
所以![]() 是指数型数列.
是指数型数列.
![]() Ⅱ
Ⅱ![]() 证明:由题意,
证明:由题意,![]() 是“指数型数列”,
是“指数型数列”,
![]() ,
,![]() ,
,
所以数列![]() 是等比数列,
是等比数列,![]() ,
,
![]() ,数列
,数列![]() 是“指数型数列”.
是“指数型数列”.
![]() Ⅲ
Ⅲ![]() 证明:因为数列
证明:因为数列![]() 是指数型数列,故对于任意的n,
是指数型数列,故对于任意的n,![]() ,
,
有![]() ,
,![]() ,
,
假设数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 构成等差数列,不妨设
构成等差数列,不妨设![]() ,
,
则由![]() ,得
,得![]() ,
,
所以![]() ,
,
当a为偶数时,![]() 是偶数,而
是偶数,而![]() 是偶数,
是偶数,![]() 是奇数,
是奇数,
故![]() 不能成立;
不能成立;
当a为奇数时,![]() 是偶数,而
是偶数,而![]() 是奇数,
是奇数,![]() 是偶数,
是偶数,
故![]() 也不能成立.
也不能成立.
所以,对任意![]() ,
,![]() 不能成立,
不能成立,
即数列![]() 的任意三项都不成构成等差数列.
的任意三项都不成构成等差数列.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 与抛物线
与抛物线![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(1)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(2)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某区“创文明城区”![]() 简称“创城”
简称“创城”![]() 活动中,教委对本区A,B,C,D四所高中校按各校人数分层抽样调查,将调查情况进行整理后制成如表:
活动中,教委对本区A,B,C,D四所高中校按各校人数分层抽样调查,将调查情况进行整理后制成如表:
学校 | A | B | C | D |
抽查人数 | 50 | 15 | 10 | 25 |
“创城”活动中参与的人数 | 40 | 10 | 9 | 15 |
![]() 注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值
注:参与率是指:一所学校“创城”活动中参与的人数与被抽查人数的比值![]()
假设每名高中学生是否参与“创城”活动是相互独立的.
![]() Ⅰ
Ⅰ![]() 若该区共2000名高中学生,估计A学校参与“创城”活动的人数;
若该区共2000名高中学生,估计A学校参与“创城”活动的人数;
![]() Ⅱ
Ⅱ![]() 在随机抽查的100名高中学生中,从A,C两学校抽出的高中学生中各随机抽取1名学生,求恰有1人参与“创城”活动的概率;
在随机抽查的100名高中学生中,从A,C两学校抽出的高中学生中各随机抽取1名学生,求恰有1人参与“创城”活动的概率;
![]() Ⅲ
Ⅲ![]() 若将表中的参与率视为概率,从A学校高中学生中随机抽取3人,求这3人参与“创城”活动人数的分布列及数学期望.
若将表中的参与率视为概率,从A学校高中学生中随机抽取3人,求这3人参与“创城”活动人数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,PA=1,点M是棱PC上的一点,且AM⊥PB.
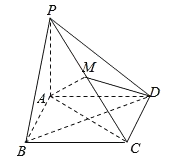
(1)求三棱锥C﹣PBD的体积;
(2)证明:AM⊥平面PBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() ,
,![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆.在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,点
,点![]() 满足
满足![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A.![]() 的方程为
的方程为![]()
B.在![]() 上存在点
上存在点![]() ,使得
,使得![]()
C.当![]() ,
,![]() ,
,![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D.在三棱锥中![]() ,
,![]() 面
面![]() ,且
,且![]() ,
,![]() ,
,![]() ,该三棱锥体积最大值为12
,该三棱锥体积最大值为12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.

(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AB=1,BC=2,AC![]() ,PC
,PC![]() ,PA
,PA![]() ,PB
,PB![]() ,E是线段BC的中点.
,E是线段BC的中点.
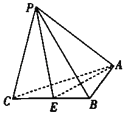
(1)求点C到平面APE的距离d;
(2)求二面角P﹣EA﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com