
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 乙图
乙图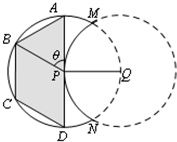
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 3 |


科目:高中数学 来源:2011届江苏省南通市高三第一次调研测试数学文卷 题型:解答题
(本小题满分16分)
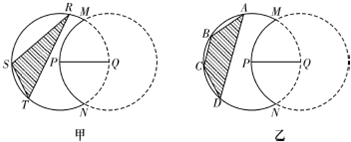
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现 要在公园内建一块顶点都在圆P上的多边形活动场地.
要在公园内建一块顶点都在圆P上的多边形活动场地.
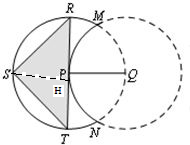
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
查看答案和解析>>
科目:高中数学 来源:2011届江苏省南通市高三第二次模拟考试数学试题 题型:解答题
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的
半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积; (2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南通市高三第二次模拟考试数学试题 题型:解答题
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的
半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
 (2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com