
【题目】(1)研究函数f(x)![]() 在(0,π)上的单调性;
在(0,π)上的单调性;
(2)求函数g(x)=x2+πcosx的最小值.
【答案】(1)f(x)在(0,π )递减;(2)![]() .
.
【解析】
(1)根据![]() ,求导得
,求导得![]() ,设m(x)=xcos x﹣sinx,x∈(0,π),通过求导来判断其正负,从而得到f′(x)的正负,进而研究f(x)的单调性.
,设m(x)=xcos x﹣sinx,x∈(0,π),通过求导来判断其正负,从而得到f′(x)的正负,进而研究f(x)的单调性.
(2)易知g(x)是偶函数,故只需求x∈[0,+∞)时g(x)的最小值,求导得g′(x)=2x﹣πsin x,根据sinx的特点,分x∈(0,![]() )和
)和![]() 时两种情况讨论g(x)单调性,进而求其最小值.
时两种情况讨论g(x)单调性,进而求其最小值.
(1)因为![]() ,所以
,所以![]() ,
,
设m(x)=xcos x﹣sinx,x∈(0,π),
m′(x)=﹣xsin x<0,
所以m(x)在(0,π )递减,则m(x)<m(0)=0
故f′(x)<0,所以f(x)在(0,π )递减;
(2)观察知g(x)为偶函数,故只需求x∈[0,+∞)时g(x)的最小值,
由g′(x)=2x﹣πsin x,当x∈(0,![]() ) 时,设n(x)=2x﹣π sin x,则n′(x)=2﹣π cos x,显然 n′(x) 递增,
) 时,设n(x)=2x﹣π sin x,则n′(x)=2﹣π cos x,显然 n′(x) 递增,
而n′(0)=2﹣π<0,![]() ,
,
由零点存在定理,存在唯一的![]() ,使得n′(x0)=0
,使得n′(x0)=0
当x∈(0,x0)时,n′(x)<0,n(x)递减,
当![]() 时,n′(x)>0,n(x)递增,
时,n′(x)>0,n(x)递增,
而n(0)=0,![]() ,故
,故![]() 时,n(x)<0,
时,n(x)<0,
即![]() 时,g′(x)<0,则g(x)递减;
时,g′(x)<0,则g(x)递减;
又当![]() 时,2x>π>π sin x,g′(x)>0,g(x) 递增;
时,2x>π>π sin x,g′(x)>0,g(x) 递增;
所以![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】某蔬菜批发商经销某种新鲜蔬菜(以下简称![]() 蔬菜),购入价为200元/袋,并以300元/袋的价格售出,若前8小时内所购进的
蔬菜),购入价为200元/袋,并以300元/袋的价格售出,若前8小时内所购进的![]() 蔬菜没有售完,则批发商将没售完的
蔬菜没有售完,则批发商将没售完的![]() 蔬菜以150元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
蔬菜以150元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 蔬菜低价处理完,且当天不再购进).该蔬菜批发商根据往年的销量,统计了100天
蔬菜低价处理完,且当天不再购进).该蔬菜批发商根据往年的销量,统计了100天![]() 蔬菜在每天的前8小时内的销售量,制成如下频数分布条形图.
蔬菜在每天的前8小时内的销售量,制成如下频数分布条形图.

(1)若某天该蔬菜批发商共购入6袋![]() 蔬菜,有4袋
蔬菜,有4袋![]() 蔬菜在前8小时内分别被4名顾客购买,剩下2袋在8小时后被另2名顾客购买.现从这6名顾客中随机选2人进行服务回访,则至少选中1人是以150元/袋的价格购买的概率是多少?
蔬菜在前8小时内分别被4名顾客购买,剩下2袋在8小时后被另2名顾客购买.现从这6名顾客中随机选2人进行服务回访,则至少选中1人是以150元/袋的价格购买的概率是多少?
(2)以上述样本数据作为决策的依据.
(i)若今年![]() 蔬菜上市的100天内,该蔬菜批发商坚持每天购进6袋
蔬菜上市的100天内,该蔬菜批发商坚持每天购进6袋![]() 蔬菜,试估计该蔬菜批发商经销
蔬菜,试估计该蔬菜批发商经销![]() 蔬菜的总盈利值;
蔬菜的总盈利值;
(ii)若明年该蔬菜批发商每天购进![]() 蔬菜的袋数相同,试帮其设计明年的
蔬菜的袋数相同,试帮其设计明年的![]() 蔬菜的进货方案,使其所获取的平均利润最大.
蔬菜的进货方案,使其所获取的平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρ2﹣6ρcosθ+5=0,曲线C2的参数方程为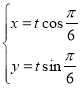 (t为参数).
(t为参数).
(1)求曲线C1的直角坐标方程,并说明是什么曲线?
(2)若曲线C1与C2相交于A、B两点,求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方形SG1G2G3中,E、F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE、SF及EF把这个正方形折成一个四面体,使G1、G2、G3三点重合,重合后的点记为G,那么,在四面体S﹣EFG中必有( )
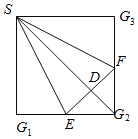
A.SG⊥△EFG所在平面B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面D.GD⊥△SEF所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
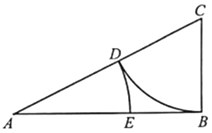
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、点
、点![]() 及抛物线
及抛物线![]() .
.
(1)若直线![]() 过点
过点![]() 及抛物线
及抛物线![]() 上一点
上一点![]() ,当
,当![]() 最大时求直线
最大时求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得过点
,使得过点![]() 的任一条直线与抛物线
的任一条直线与抛物线![]() 交于点
交于点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离相等?若存在,求出点
的距离相等?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下(提示:可以用第(2)问的结论),任意的![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com