Question

15．过y²=4x的焦点作直线交抛物线于A，B两点，若O为坐标原点，则$\overrightarrow{OA}$•$\overrightarrow{OB}$=（　　）

• A． -1
• B． -2
• C． -3
• D． 不确定

Answer 1

分析 可得出抛物线y²=4x的焦点为（1，0），并画出图形，根据题意可设AB的方程为x=ky+1，联立抛物线方程消去x便得到y²-4ky-4=0，从而得出y₁y₂=-4，然后可设$A（\frac{{{y}_{1}}^{2}}{4}，{y}_{1}），B（\frac{{{y}_{2}}^{2}}{4}，{y}_{2}）$，这样便可求出$\overrightarrow{OA}•\overrightarrow{OB}$的值．

解答 解：抛物线y²=4x的焦点坐标为（1，0），如图：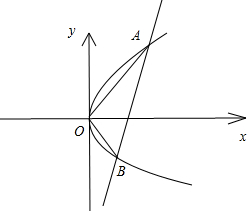
设直线AB的方程为x=ky+1，代入y²=4x消去x得：
y²-4ky-4=0；
∴y₁y₂=-4；
设$A（\frac{{{y}_{1}}^{2}}{4}，{y}_{1}），B（\frac{{{y}_{2}}^{2}}{4}，{y}_{2}）$，则：
$\overrightarrow{OA}•\overrightarrow{OB}=\frac{{（y}_{1}{y}_{2}）^{2}}{16}+{y}_{1}{y}_{2}=\frac{16}{16}-4=-3$．
故选C．

点评 考查抛物线的标准方程，过定点且斜率不为0的直线方程的设法，韦达定理，以及向量数量积的坐标运算．