
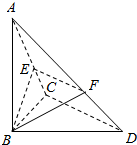
 已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).
已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).分析 (1)由已知中,∠BCD=90°,AB⊥平面BCD,我们易得到CD⊥平面ABC,又由E、F分别是AC、AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).故EF∥CD即EF⊥平面ABC,再由面面垂直的判定定理,即可得到答案.
(2)由(1)知,BE⊥EF,又平面BEF⊥平面ACD,BE⊥平面ACD,BE⊥AC.故只须让所求λ的值能证明BE⊥AC即可.在△ABC中求出k的值.
(3)由VA-BEF=VB-AEF,利用等体积法能求出三棱锥A-BEF的体积.
解答 (1)证明:∵AB⊥平面BCD,
∴AB⊥CD,
又在△BCD中,∠BCD=90°,
∴BC⊥CD,又AB∩BC=B,
∴CD⊥平面ABC,
又在△ACD中E、F分别是AC、AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).
∴EF∥CD,
∴EF⊥平面ABC,又EF?平面BEF,
∴不论k为何值,总有平面BEF⊥平面ABC.
(2)解:由(1)知,BE⊥EF,又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC.
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=$\sqrt{2}$,AB=$\sqrt{2}$tan60°=$\sqrt{6}$,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{7}$,
由AB2=AE•AC,得AE=$\frac{6}{\sqrt{7}}$,∴k=$\frac{AE}{AC}$=$\frac{6}{7}$,
故当k=$\frac{6}{7}$时,平面BEF⊥平面ACD.
(3)∵BE⊥AC,AB⊥AC,∴$BE=\frac{AB•BC}{AC}$=$\frac{\sqrt{6}×1}{\sqrt{7}}$=$\frac{\sqrt{6}}{\sqrt{7}}$,
∵AC⊥CD,EF∥CD,∴AE⊥EF,∴S△AEF=$\frac{1}{2}×AE×EF$=$\frac{1}{2}×\frac{6}{\sqrt{7}}×\frac{6}{7}$=$\frac{18}{7\sqrt{7}}$,
∴三棱锥A-BEF的体积VA-BEF=VB-AEF=$\frac{1}{3}×\frac{\sqrt{6}}{\sqrt{7}}×\frac{18}{7\sqrt{7}}$=$\frac{6\sqrt{6}}{49}$.
点评 本题考查了面面垂直的判定,考查三棱锥的体积的求法,在证明面面垂直时,其常用方法是在其中一个平面内找两条相交直线和另一平面内的某一条直线垂直.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
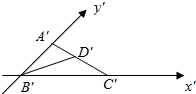 如图所示,水平放置的△ABC在坐标系中的直观图,其中D′是A′C′的中点,且∠ACB≠30°,则原图形中与线段BD的长相等的线段有2条.
如图所示,水平放置的△ABC在坐标系中的直观图,其中D′是A′C′的中点,且∠ACB≠30°,则原图形中与线段BD的长相等的线段有2条.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com