
【题目】如果数列![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ),满足:①
),满足:①![]() ,
,![]() ;
;
②![]() ,那么称数列
,那么称数列![]() 为“
为“![]() ”数列.
”数列.
(![]() )已知数列
)已知数列![]() ,
,![]() ,
,![]() ,
,![]() ;数列
;数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试判断数列
.试判断数列![]() ,
,![]() 是否为“
是否为“![]() ”数列.
”数列.
(![]() )是否存在一个等差数列是“
)是否存在一个等差数列是“![]() ”数列?请证明你的结论.
”数列?请证明你的结论.
(![]() )如果数列
)如果数列![]() 是“
是“![]() ”数列,求证:数列
”数列,求证:数列![]() 中必定存在若干项之和为
中必定存在若干项之和为![]() .
.
【答案】(![]() )数列
)数列![]() 不是“
不是“![]() ”数列,数列
”数列,数列![]() 是“
是“![]() ”数列;(
”数列;(![]() )不存在等差数列是“
)不存在等差数列是“![]() ”数列;(
”数列;(![]() )证明见解析.
)证明见解析.
【解析】分析:(1)根据定义直接判断即可得解;(2)假设存在等差数列是“![]() ”数列,由
”数列,由![]() ,得
,得![]() ,与
,与![]() 矛盾,从而可证不存在等差数列为“
矛盾,从而可证不存在等差数列为“![]() ”数列;(3)将数列
”数列;(3)将数列![]() 按以下方法重新排列:设
按以下方法重新排列:设![]() 为重新排列后所得数列的前
为重新排列后所得数列的前![]() 项和(
项和(![]() 且
且![]() ),任取大于0的一项作为第一项,则满足
),任取大于0的一项作为第一项,则满足![]() ,然后利用反证法,证明即可.
,然后利用反证法,证明即可.
详解:(![]() )由题目是
)由题目是![]() 定义可直接判断出,数列
定义可直接判断出,数列![]() 不符合
不符合![]() 数列要求,数列
数列要求,数列![]() 是“
是“![]() ”数列.
”数列.
(![]() )不存在一个等差数列是“
)不存在一个等差数列是“![]() ”数列,
”数列,
证明:假设存在等差数列是“![]() ”数列,
”数列,
则由![]() ,得
,得![]() 与
与![]() 矛盾,
矛盾,
说明假设不成立,即不存在等差数列是“![]() ”数列.
”数列.
(![]() )将数列
)将数列![]() 按以下方法重新排列:
按以下方法重新排列:
设![]() 为重新排列后所得数列的前
为重新排列后所得数列的前![]() 项和(
项和(![]() ,且
,且![]() ),
),
任取大于![]() 的一项作为第一项,则满足
的一项作为第一项,则满足![]() ,
,
假设当![]() 时,
时,![]() ,
,
若![]() ,则任取大于
,则任取大于![]() 的一项作为第
的一项作为第![]() 项,可保证
项,可保证![]() ,
,
若![]() ,则剩下的项必有
,则剩下的项必有![]() 或与
或与![]() 异号的一项,否则总和不是
异号的一项,否则总和不是![]() ,
,
∴取![]() 或与
或与![]() 异号的一项作为第
异号的一项作为第![]() 项,可保证
项,可保证![]() ,
,
如果按上述排列后存在![]() 成立,那么命题得证,
成立,那么命题得证,
否则![]() ,
,![]() ,
,![]()
![]() 这
这![]() 个整数只能取区间
个整数只能取区间![]() 内的非
内的非![]() 整数,
整数,
∵区间![]() 内的非
内的非![]() 整数至多
整数至多![]() 个,
个,
∴一定存在![]() ,
,
那么从第![]() 项到第
项到第![]() 项之和为
项之和为![]() ,命题得证,
,命题得证,
综上所述,数列![]() 中一定存在若干项之和为
中一定存在若干项之和为![]() ,证毕.
,证毕.


科目:高中数学 来源: 题型:
【题目】已知命题![]() 函数
函数![]() 是
是![]() 上的奇函数,命题
上的奇函数,命题![]() 函数
函数![]() 的定义域和值域都是
的定义域和值域都是![]() ,其中
,其中![]() .
.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的值;
的值;
(2)若“![]() 且
且![]() ”为假命题,“
”为假命题,“![]() 或
或![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商场对前5天抽奖活动的人数进行统计,y表示第x天参加抽奖活动的人数,得到统计表如下:
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析,发现y与x具有线性相关关系.
(1)若从这5天随机抽取两天,求至少有1天参加抽奖人数超过70的概率;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,并估计该活动持续7天,共有多少名顾客参加抽奖?
,并估计该活动持续7天,共有多少名顾客参加抽奖?
参考公式及数据: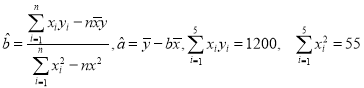 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和是Sn , 且Sn+ ![]() an=1,数列{bn},{cn}满足bn=log3
an=1,数列{bn},{cn}满足bn=log3 ![]() ,cn=
,cn= ![]() . (Ⅰ)求数列{an}的通项公式;
. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{cn}的前n项和为Tn , 若不等式Tn<m对任意的正整数n恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)在线段EF上是否存在一点P,使得平面PAB与平面ADE所成的锐二面角的余弦值为 ![]() .若存在,求出点P的位置;若不存在,说明理由.
.若存在,求出点P的位置;若不存在,说明理由.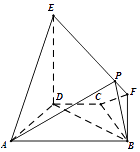
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+ ![]() x2﹣ax(a为常数)有两个极值点.
x2﹣ax(a为常数)有两个极值点.
(1)求实数a的取值范围;
(2)设f(x)的两个极值点分别为x1 , x2 , 若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且满足S4=24,S7=63. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2sinxcosx+3cos2x. (Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若x∈[0, ![]() ],求函数f(x)的最值及相应x的取值.
],求函数f(x)的最值及相应x的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com