
【题目】定义在R上的函数y=f(x),恒有f(x)=f(2﹣x)成立,且f′(x)(x﹣1)>0,对任意的x1<x2 , 则f(x1)<f(x2)成立的充要条件是( )
A.x2>x1≥1
B.x1+x2>2
C.x1+x2≤2
D.x2 ![]()
【答案】B
【解析】解:由f(x)=f(2﹣x),得函数关于x=1对称.由f'(x)(x﹣1)>0得,当x>1时,f′(x)>0,此时函数为增函数;当x<1时,f′(x)<0,此时函数f(x)为减函数,
①若x1<x2,当1≤x1,函数为增函数,满足对任意的x1<x2,f(x1)<f(x2),此时x1+x2>2,
②若x1<1,
∵函数f(x)关于x=1对称,则f(x1)=f(2﹣x1),则2﹣x1>1,
则由f(2﹣x1)=f(x1)<f(x2),此时2﹣x1<x2,即x1+x2>2,
即对任意的x1<x2,f(x1)<f(x2)得x1+x2>2,反之也成立,
即对任意的x1<x2,f(x1)<f(x2)是x1+x2>2的充要条件,
所以答案是:B
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】将一张边长为12cm的正方形纸片按如图(1)所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型,如图(2)所示放置.如果正四棱锥的主视图是等边三角形,如图(3)所示,则正四棱锥的体积是( ) 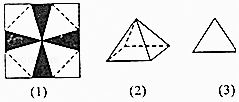
A.![]() cm3
cm3
B.![]() cm3
cm3
C.![]() cm3
cm3
D.![]() cm3
cm3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
A.55π
B.75π
C.77π
D.65π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)当x∈[2,4]时.求该函数的值域;
(2)若f(x)≥mlog2x对于x∈[4,16]恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点D是椭圆C: ![]() =1(a>b>0)上一点,F1 , F2分别为C的左、右焦点,|F1F2|=2
=1(a>b>0)上一点,F1 , F2分别为C的左、右焦点,|F1F2|=2 ![]() ,∠F1DF2=60°,△F1DF2的面积为
,∠F1DF2=60°,△F1DF2的面积为 ![]()
(1)求椭圆C的方程;
(2)过点Q(1,0)的直线l与椭圆C相交于A,B两点,点P(4,3),记直线PA,PB的斜率分别为k1 , k2 , 当k1k2最大时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年射阳县洋马镇政府决定投资8千万元启动“鹤乡菊海”观光旅游及菊花产业项目.规划从2017年起,在相当长的年份里,每年继续投资2千万元用于此项目.2016年该项目的净收入为5百万元(含旅游净收入与菊花产业净收入),并预测在相当长的年份里,每年的净收入均为上一年的1.5倍.记2016年为第1年,f(n)为第1年至此后第n(n∈N*)年的累计利润(注:含第n年,累计利润=累计净收入﹣累计投入,单位:千万元),且当f(n)为正值时,认为该项目赢利.
(1)试求f(n)的表达式;
(2)根据预测,该项目将从哪一年开始并持续赢利?请说明理由.
(参考数据: ![]() ,ln2≈0.7,ln3≈1.1)
,ln2≈0.7,ln3≈1.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n≥3,n∈N* , 在集合{1,2,…,n}的所有元素个数为2的子集中,把每个子集的较大元素相加,和记为a,较小元素之和记为b.
(1)当n=3时,求a,b的值;
(2)求证:对任意的n≥3,n∈N* , ![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com