
【题目】已知数列{an}中各项都大于1,前n项和为Sn , 且满足an2+3an=6Sn﹣2.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
【答案】
(1)解:由an2+3an=6Sn﹣2,即6Sn=an2+3an+2,
当n≥2时,6Sn﹣1=an﹣12+3an﹣1+2,
两式相减得:6an=an2﹣an﹣12+3an﹣3an﹣1,整理得:an2﹣an﹣12=3an+3an﹣1,
即(an+an﹣1)(an﹣an﹣1)=3(an+an﹣1),
∵数列{an}中各项都大于1,
∴an+an﹣1≠0,
∴an﹣an﹣1=3,
当n=1时,a12+3a1=6S1﹣2.解得:a1=2,
∴数列{an}是以2为首项,以3为公差的等差数列,
∴an=2+3(n﹣1)=3n﹣1,
∴数列{an}的通项公式an=3n﹣1
(2)解:bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
数列{bn}的前n项和Tn,Tn=b1+b2+b3+…+bn,
= ![]() [(
[( ![]() ﹣
﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…+(
)+…+( ![]() ﹣
﹣ ![]() )],
)],
= ![]() (
( ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() ),
),
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
= ![]() ,
,
Tn= ![]()
(3)解:Tn< ![]() 对所有n∈N*都成立的最小正整数m,
对所有n∈N*都成立的最小正整数m,
Tn= ![]() (
( ![]() ﹣
﹣ ![]() )<
)< ![]() ×
× ![]() =
= ![]() ,
,
即 ![]() ≥
≥ ![]() ,即m≥6
,即m≥6
∴所有n∈N*对所有n∈N*都成立的最小正整数m=6
【解析】【(1)由6Sn=an2+3an+2,当n≥2时,6Sn﹣1=an﹣12+3an﹣1+2,an2﹣an﹣12=3an+3an﹣1 , 即(an+an﹣1)(an﹣an﹣1)=3(an+an﹣1),由an+an﹣1≠0,an﹣an﹣1=3,当n=1时,a1=2,根据等差数列的通项公式,即可求得数列{an}的通项公式;(2)bn= ![]() =
= ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),利用“裂项法”即可求得数列{bn}的前n项和Tn;(3)由题意可得Tn=
),利用“裂项法”即可求得数列{bn}的前n项和Tn;(3)由题意可得Tn= ![]() (
( ![]() ﹣
﹣ ![]() )<
)< ![]() ×
× ![]() =
= ![]() ,即
,即 ![]() ≥
≥ ![]() ,即可求得对所有n∈N*都成立的最小正整数m.
,即可求得对所有n∈N*都成立的最小正整数m.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


科目:高中数学 来源: 题型:
【题目】一企业从某生产线上随机抽取40件产品,测量这些产品的某项技术指标值![]() ,得到如下的频数表
,得到如下的频数表
|
|
|
|
|
频数 | 3 | 15 | 17 | 5 |
(1)估计该技术指标值的平均数(以各组区间中点值为代表);
(2)若![]() ,则该产品不合格,其余合格产品。产生一件产品,若是合格品,可盈利100元,若不是合格品则亏损20元。从该生产线生产的产品中任取2件,记
,则该产品不合格,其余合格产品。产生一件产品,若是合格品,可盈利100元,若不是合格品则亏损20元。从该生产线生产的产品中任取2件,记![]() 为这2件产品的总利润,求随机变量
为这2件产品的总利润,求随机变量![]() 的分布列和期望值。
的分布列和期望值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(﹣x)=8﹣f(4+x),函数g(x)= ![]() ,若函数f(x)与g(x)的图象共有168个交点,记作Pi(xi , yi)(i=1,2,…,168),则(x1+y1)+(x2+y2)+…+(x168+y168)的值为( )
,若函数f(x)与g(x)的图象共有168个交点,记作Pi(xi , yi)(i=1,2,…,168),则(x1+y1)+(x2+y2)+…+(x168+y168)的值为( )
A.2018
B.2017
C.2016
D.1008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC中角A,B,C的对边,且csinB= ![]() bcosC.
bcosC.
(1)求角C的大小;
(2)若c=3,sinA=2sinB,求△ABC的面积S△ABC .
查看答案和解析>>
科目:高中数学 来源: 题型:
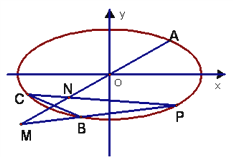
【题目】如图,在平面直角坐标系中,已知A、B、C是椭圆![]() 上不同的三点,
上不同的三点,  ,C在第三象限,线段BC的中点在直线OA上。
,C在第三象限,线段BC的中点在直线OA上。
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A、B、C)且直线PB, PC分别交直线OA于M、N两点,证明![]() 为定值并求出该定值.
为定值并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是( )
A.[﹣5,﹣3]
B.[﹣6,﹣ ![]() ]
]
C.[﹣6,﹣2]
D.[﹣4,﹣3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型 | 木地板A | 木地板B | 木地板C |
环保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com