

 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,讨论
时,讨论 的单调性.
的单调性.
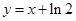 ;(2)详见解析.
;(2)详见解析. 代入得到
代入得到 表达式,对
表达式,对 求导,将切点的横坐标2代入
求导,将切点的横坐标2代入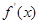 中得到切线的斜率k,再将切点的横坐标2代入到
中得到切线的斜率k,再将切点的横坐标2代入到 中,得到切点的纵坐标,最后利用点斜式写出切线方程;第二问,讨论
中,得到切点的纵坐标,最后利用点斜式写出切线方程;第二问,讨论 的单调性即讨论
的单调性即讨论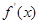 的正负,即讨论导数表达式分子的正负,所以构造函数
的正负,即讨论导数表达式分子的正负,所以构造函数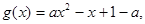 ,通过分析题意,将
,通过分析题意,将 分成
分成 、
、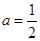 、
、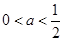 、
、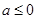 多种情况,分类讨论,判断
多种情况,分类讨论,判断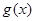 的正负,从而得到
的正负,从而得到 的单调性.
的单调性.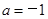 时,
时,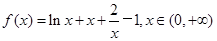
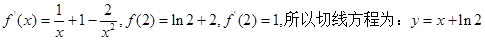 6分
6分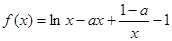 ,
,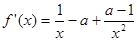
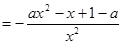
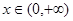 ,
,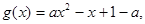
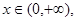 8分
8分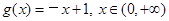
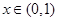 时g(x)>0,
时g(x)>0, 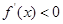 此时函数
此时函数 单调递减,
单调递减,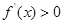 此时函数f,(x)单调递增。
此时函数f,(x)单调递增。 时,由
时,由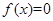 ,解得:
,解得: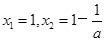 10分
10分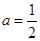 ,函数f(x)在
,函数f(x)在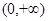 上单调递减, 11分
上单调递减, 11分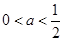 ,在
,在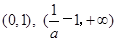 单调递减,在
单调递减,在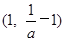 上单调递增.
上单调递增.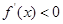 ,函数f(x)单调递减;
,函数f(x)单调递减;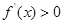 ,此时函数
,此时函数 单调递增。
单调递增。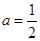 时,函数f(x)在(0, + ∞)上单调递减
时,函数f(x)在(0, + ∞)上单调递减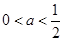 时,函数f(x)在
时,函数f(x)在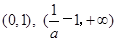 上单调递减;
上单调递减; 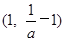 上单调递增; 14分
上单调递增; 14分

科目:高中数学 来源:不详 题型:解答题
 ,函数
,函数 .
. 时,函数
时,函数 的图象与函数
的图象与函数 的图象有公共点,求实数
的图象有公共点,求实数 的最大值;
的最大值; 时,试判断函数
时,试判断函数 的图象与函数
的图象与函数 的图象的公共点的个数;
的图象的公共点的个数; 的图象能否恒在函数
的图象能否恒在函数 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 1 |
| 3 |
| 1 |
| 2 |
| A.a-b<-3 | B.a-b≤-3 | C.a-b>-3 | D.a-b≥-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com