
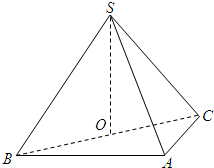
 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 ,∠BAC=90°,O为BC中点.
,∠BAC=90°,O为BC中点.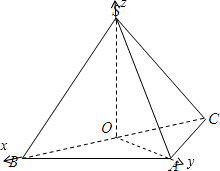 解:(Ⅰ)因为SB=SC,O为BC中点,所以SO⊥BC
解:(Ⅰ)因为SB=SC,O为BC中点,所以SO⊥BC ,0,0),A(0,
,0,0),A(0, ,0),S(0,0,
,0),S(0,0, ),C(-
),C(- ,0,0),
,0,0),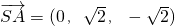 ,
,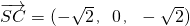 ,
,
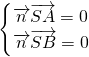 ,∴
,∴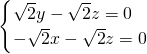 ,可取
,可取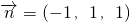
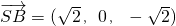 ,故点B到平面SAC的距离d=|
,故点B到平面SAC的距离d=|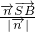 |=
|=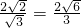
 =(0,1,0),平面SAC的法向量
=(0,1,0),平面SAC的法向量 =(-1,1,1)
=(-1,1,1) =
= =
= .
.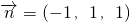 ,而
,而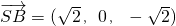 ,从而可求点B到平面SAC的距离d=|
,从而可求点B到平面SAC的距离d=|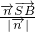 |;
|; =(0,1,0),平面SAC的法向量
=(0,1,0),平面SAC的法向量 =(-1,1,1),从而可得二面角A-SC-B的余弦值.
=(-1,1,1),从而可得二面角A-SC-B的余弦值.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com