
分析 (1)求出f′(x),令f′(x)小于0求出x的范围即为函数的减区间,令f′(x)大于0求出x的范围即为函数的增区间;
(2)当0<t<t+2<$\frac{1}{e}$时t无解,当0<t≤$\frac{1}{e}$<t+2即0<t≤$\frac{1}{e}$时,根据函数的增减性得到f(x)的最小值为f($\frac{1}{e}$),当$\frac{1}{e}$<t<t+2即t>$\frac{1}{e}$时,函数为增函数,得到f(x)的最小值为f(t);
(3)求出g′(x),把f(x)和g′(x)代入2f(x)≤g′(x)+2中,根据x大于0解出a≥lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,然后令h(x)=lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,求出h(x)的最大值,a大于等于h(x)的最大值,方法是先求出h′(x)=0时x的值,利用函数的定义域和x的值分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性即可得到函数的最大值,即可求出a的取值范围.
解答 解:(1)f′(x)=lnx+1令f′(x)<0解得0<x<$\frac{1}{e}$,
∴f(x)的单调递减区间为(0,$\frac{1}{e}$)
令f′(x)>0解得x>$\frac{1}{e}$,
∴f(x)的单调递增区间为($\frac{1}{e}$,+∞);
(2)当0<t<t+2<$\frac{1}{e}$时,t无解
当0<t≤$\frac{1}{e}$<t+2,即0<t≤$\frac{1}{e}$时,
∴f(x)min=f($\frac{1}{e}$)=-$\frac{1}{e}$;
当$\frac{1}{e}$<t<t+2,即t>$\frac{1}{e}$时,f(x)在[t,t+2]上单调递增,
∴f(x)min=f(t)=tlnt
∴f(x)min=$\left\{\begin{array}{l}{-\frac{1}{e},0<t≤\frac{1}{e}}\\{tlnt,t>\frac{1}{e}}\end{array}\right.$;
(3)由题意:2xlnx≤3x2+2ax-1+2即2xlnx≤3x2+2ax+1
∵x∈(0,+∞)
∴a≥lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,
设h(x)=lnx-$\frac{3}{2}$x-$\frac{1}{2x}$,
则h′(x)=$\frac{1}{x}$-$\frac{3}{2}$+$\frac{1}{{2x}^{2}}$=-$\frac{(x-1)(3x+1)}{{2x}^{2}}$,
令h′(x)=0,得x=1,x=-$\frac{1}{3}$(舍)
当0<x<1时,h′(x)>0;当x>1时,h′(x)<0
∴当x=1时,h(x)取得最大值,h(x)max=-2
∴a≥-2
故实数a的取值范围[-2,+∞).
点评 本题要求学生会利用导函数的正负得到函数的额单调区间以及会根据函数的增减性得到函数的极值,掌握不等式恒成立时所满足的条件,是一道中档题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
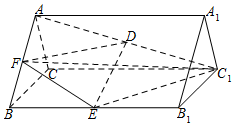 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两解 | B. | 一解 | C. | 无解 | D. | 无穷多解 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 9 | D. | -9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com