
【题目】已知点![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率及左焦点
的离心率及左焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(Ⅲ)判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.
上.
(1)求![]() 的边
的边![]() 所在的直线方程;
所在的直线方程;
(2)求![]() 的面积最小值,并求出此时点
的面积最小值,并求出此时点![]() 的坐标;
的坐标;
(3)若![]() 为线段
为线段![]() 上的任意一点,求
上的任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
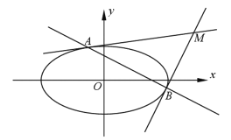
(1)求![]() 的值;
的值;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《算法统宗》中有这样一个问题:“三百一十五里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还其大意为:“有一个人走315里路,第一天健步行走,从第二天起脚痛,每天走的路程为前一天的一半,走了 6天后到达目的地. ”则该人最后一天走的路程为( )
A.20里B.10里C.5 里D.2.5 里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() 关于直线
关于直线![]() 对称.
对称.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作两条相异直线分别与圆
作两条相异直线分别与圆![]() 相交于
相交于![]() 、
、![]() 两点,若直线
两点,若直线![]() 、
、![]() 的倾斜角互补,问直线
的倾斜角互补,问直线![]() 与直线
与直线![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形![]() 沿对角线
沿对角线![]() 折成直二面角,下列结论:①异面直线
折成直二面角,下列结论:①异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④二面角
是等边三角形;④二面角![]() 的平面角正切值是
的平面角正切值是![]() ;其中正确结论是______.(写出你认为正确的所有结论的序号)
;其中正确结论是______.(写出你认为正确的所有结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com