
 ,令
,令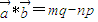 .给出以下四个命题:(1)若
.给出以下四个命题:(1)若 与
与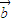 共线,则
共线,则 ;(2)
;(2) ;(3)对任意的λ∈R,有
;(3)对任意的λ∈R,有 ;(4)
;(4) =
= .(注:这里
.(注:这里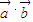 指
指 与
与 的数量积)其中所有真命题的序号是 .
的数量积)其中所有真命题的序号是 . 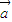 =(x,y),∵若
=(x,y),∵若 与
与 共线,则
共线,则  =(λx,λy ),
=(λx,λy ),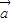 *
* =x•λy-y•λx=0,故(1)正确;
=x•λy-y•λx=0,故(1)正确;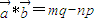 ,而
,而 =np-mq,故(2)不正确;
=np-mq,故(2)不正确; *
* =(λm,λn )*(p,q)=λmq-λnp,
=(λm,λn )*(p,q)=λmq-λnp,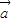 *
* )=λ (mq-np)=λmq-λnp,∴
)=λ (mq-np)=λmq-λnp,∴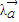 *
* =λ(
=λ( 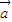 *
* ) 成立,故(3)正确;
) 成立,故(3)正确; +
+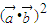 =(mq-np)2+(mp+nq)2=m2q2+n2p2+m2p2+n2q2,
=(mq-np)2+(mp+nq)2=m2q2+n2p2+m2p2+n2q2, =(m2+n2)(p2+q2)=m2q2+n2p2+m2p2+n2q2,故(4)正确.
=(m2+n2)(p2+q2)=m2q2+n2p2+m2p2+n2q2,故(4)正确.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
A、若
| ||||||||||||
B、
| ||||||||||||
C、对任意的λ∈R,有(λ
| ||||||||||||
D、(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、(1)(2)(3) |
| B、(2)(3)(4) |
| C、(1)(3)(4) |
| D、(1)(2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| ON |
| ON |
A、
| ||
B、2+
| ||
C、2-
| ||
| D、2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com