


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省高二下学期第一次月考数学(理) 题型:填空题
16.某校有6间不同的电脑室,每天晚上至少开放2间,求不同安排方案的种数,现有四位同学分别给出下列四个结果①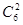 ②
②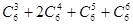 ③
③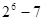 ④
④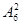 其中正确的结论是___
其中正确的结论是___
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com