Question

12．一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A测得水柱顶端的仰角为45°，沿点A向北偏东30°前进100米到达点B，在B点测得水柱顶端的仰角为30°，则水柱的高度是（　　）

• A． 50米
• B． 60米
• C． 80米
• D． 100米

Answer 1

分析 如图所示，设水柱CD的高度为h．在Rt△ACD中，由∠DAC=45°，可得AC=h．由∠BAE=30°，可得∠CAB=60°．在Rt△BCD中，∠CBD=30°，可得BC=$\sqrt{3}h$．在△ABC中，由余弦定理可得：BC²=AC²+AB²-2AC•ABcos60°．代入即可得出．

解答 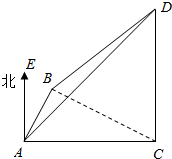解：如图所示，
设水柱CD的高度为h．
在Rt△ACD中，∵∠DAC=45°，∴AC=h．
∵∠BAE=30°，∴∠CAB=60°．
在Rt△BCD中，∠CBD=30°，∴BC=$\sqrt{3}h$．
在△ABC中，由余弦定理可得：BC²=AC²+AB²-2AC•ABcos60°．
∴（$\sqrt{3}h$）²=h²+100²-$2×100h×\frac{1}{2}$，
化为h²+50h-5000=0，解得h=50．
故选：A．

点评 本题考查了直角三角形的边角关系、余弦定理，考查了推理能力和计算能力，属于中档题．