
分析 (Ⅰ)利用两角差的余弦公式展开,利用辅助角公式即可求得f(x),根据周期公式,即可求得函数f(x)的最小正周期;
(Ⅱ)利用正弦定理,求得B=$\frac{π}{3}$,则0<A<$\frac{2π}{3}$,根据正弦函数的性质即可求得$f(\frac{A}{2})$的取值范围.
解答 解:(Ⅰ)由$f(x)=cos(2x-\frac{π}{6})+sin2x$=cos2xcos$\frac{π}{6}$+sin2xsin$\frac{π}{6}$+sin2x,
=$\frac{3}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x,
=$\sqrt{3}$sin(2x+$\frac{π}{6}$),
则f(x)的最小正周期T=$\frac{2π}{ω}$=π;
(Ⅱ)由正弦定理:$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,则a=2RsinA,b=2RsinB,c=2RsinC,
由(2a-c)cosB=bcosC,则(2sinA-sinC)cosB=sinBcosC,则2sinAcosB=sin(B+C),
由sin(B+C)=sin(π-A)=sinA>0,
∴cosB=$\frac{1}{2}$,
由0<B<π,则B=$\frac{π}{3}$,
$f(\frac{A}{2})$=$\sqrt{3}$sin(2×$\frac{A}{2}$+$\frac{π}{6}$)=$\sqrt{3}$sin(A+$\frac{π}{6}$),
由0<A<$\frac{2π}{3}$,
则$\frac{π}{6}$<A+$\frac{π}{6}$<$\frac{5π}{6}$,
∴$\frac{1}{2}$<sin(A+$\frac{π}{6}$)≤1,则$\frac{\sqrt{3}}{2}$<$\sqrt{3}$sin(A+$\frac{π}{6}$)≤$\sqrt{3}$,
∴f(A)∈($\frac{\sqrt{3}}{2}$,$\sqrt{3}$].
点评 本题考查两角和差的余弦公式,考查正弦函数的图象及性质,考查正弦定理的应用,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
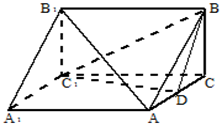 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | -8 | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4+2i | B. | -4-2i | C. | -2+4i | D. | -2+6i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin4x | B. | .y=tan2x | C. | y=cos22x-sin22x | D. | y=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0≤a≤21 | B. | a=0或a=7 | C. | a<0或a>21 | D. | a=0或a=21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,使tanx≠1 | B. | ¬p:?x∈R,使tanx≠1 | ||
| C. | ¬p:?x∉R,使tanx≠1 | D. | ¬p:?x∈R,使tanx≠1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com