
【题目】已知A(1,2),B(a,1),C(2,3),D(-1,b)(a,b∈R)是复平面上的四个点,且向量![]() 对应的复数分别为z1,z2.
对应的复数分别为z1,z2.
(1)若z1+z2=1+i,求z1,z2;
(2)若|z1+z2|=2,z1-z2为实数,求a,b的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若
(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若![]() ,
,![]() ,cos ∠ABF=
,cos ∠ABF=![]() ,则C的离心率为( )
,则C的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx﹣xcosx.
(1)讨论f(x)在(0,2π)上的单调性;
(2)若关于x的方程f(x)﹣x2+2πx﹣m=0在(0,2π)有两个根,求实数m的取值范围.
(3)求证:当x∈(0, ![]() )时,f(x)<
)时,f(x)< ![]() x3 .
x3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,D是到原点的距离不大于1的点构成的区域,E是满足不等式组 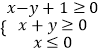 的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个说法:
①已知p,q都是命题,若p∧q为假命题,则p,q均为假命题;
②命题“若a>b,则3a>3b-1”的否命题为“若a≤b,则3a≤3b-1”;
③命题“x∈R,x2+1≥0”的否定是“x0∈R,![]() +1<0”;
+1<0”;
④“a≥0”是“x0∈R,a![]() +x0+1≥0”的充分必要条件.
+x0+1≥0”的充分必要条件.
其中正确说法的序号是 ( )
A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试.统计得到成绩与专业的列联表如下所示:
优秀 | 非优秀 | 总计 | |
A班 | 14 | 6 | 20 |
B班 | 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
则下列说法正确的是 ( )
A. 有99%的把握认为环保知识测试成绩与专业有关
B. 有99%的把握认为环保知识测试成绩与专业无关
C. 有95%的把握认为环保知识测试成绩与专业有关
D. 有95%的把握认为环保知识测试成绩与专业无关
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com