
【题目】某气象站统计了4月份甲、乙两地的天气温度(单位![]() ),统计数据的茎叶图如图所示,
),统计数据的茎叶图如图所示,
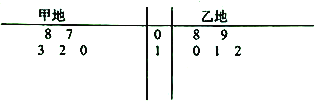
(1)根据所给茎叶图利用平均值和方差的知识分析甲,乙两地气温的稳定性;
(2)气象主管部门要从甲、乙两地各随机抽取一天的天气温度,若甲、乙两地的温度之和大于或等于![]() ,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
,则被称为“甲、乙两地往来温度适宜天气”,求“甲、乙两地往来温度适宜天气”的概率.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设数列![]() 满足
满足![]() ,其中A,B是两个确定的实数,
,其中A,B是两个确定的实数,![]()
(1)若![]() ,求
,求![]() 的前n项和;
的前n项和;
(2)证明:![]() 不是等比数列;
不是等比数列;
(3)若![]() ,数列
,数列![]() 中除去开始的两项外,是否还有相等的两项,并证明你的结论.
中除去开始的两项外,是否还有相等的两项,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月24日国家统计局在庆祝中华人民共和国成立70周年活动新闻中心举办新闻发布会指出,1952年~2018年,我国GDP查679.1亿元跃升至90.03万亿元,实际增长174倍;人均GDP从119元提高到6.46万元,实际增长70倍.全国各族人民,砥砺奋进,顽强拼搏,实现了经济社会的跨越式发展.如图是全国2010年至2018年GDP总量![]() (万亿元)的折线图.
(万亿元)的折线图.

注:年份代码1~9分别对应年份2010~2018.
(1)由折线图看出,可用线性回归模型拟合![]() 与年份代码
与年份代码![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2019年全国GDP的总量.
的回归方程(系数精确到0.01),预测2019年全国GDP的总量.
附注:参考数据:![]() ,
,![]() ,
,![]() ,
,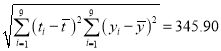 .
.
参考公式:相关系数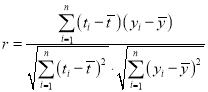 ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为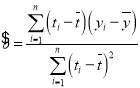 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家大力提倡科技创新,某工厂为提升甲产品的市场竞争力,对生产技术进行创新改造,使甲产品的生产节能降耗.以下表格提供了节能降耗后甲产品的生产产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)的几组对照数据.
(吨)的几组对照数据.
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(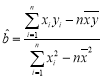 ,
,![]() )
)
(2)已知该厂技术改造前生产![]() 吨甲产品的生产能耗为
吨甲产品的生产能耗为![]() 吨,试根据(1)求出的线性回归方程,预测节能降耗后生产
吨,试根据(1)求出的线性回归方程,预测节能降耗后生产![]() 吨甲产品的生产能耗比技术改造前降低多少吨?
吨甲产品的生产能耗比技术改造前降低多少吨?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合![]() 是由一些函数组成,满足如下性质:①对任意
是由一些函数组成,满足如下性质:①对任意![]() ,
,![]() 均存在反函数
均存在反函数![]() ,且
,且![]() ;②对任意
;②对任意![]() ,方程
,方程![]() 均有解;③对任意
均有解;③对任意![]() 、
、![]() ,若函数
,若函数![]() 为定义在
为定义在![]() 上的一次函数,则
上的一次函数,则![]() .
.
(1)若![]() ,
,![]() ,均在集合
,均在集合![]() 中,求证:函数
中,求证:函数![]() ;
;
(2)若函数![]() (
(![]() )在集合
)在集合![]() 中,求实数
中,求实数![]() 的取值范围;
的取值范围;
(3)若集合![]() 中的函数均为定义在
中的函数均为定义在![]() 上的一次函数,求证:存在一个实数
上的一次函数,求证:存在一个实数![]() ,使得对一切
,使得对一切![]() ,均有
,均有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n是两条不同直线,α,β,γ是三个不同平面,给出下列四个命题:
①若m⊥α,n⊥α,则m∥n;②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若m∥α,n∥α,则m∥n;④若m⊥α,m∥β,则α⊥β.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com