
| 1 |
| bn |
| 1 |
| 3 |
| 1 |
| bn |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
| m |
| 3m+1 |
| 1 |
| 4 |
| n |
| 3n+1 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 1 |
| bn |
| 1 |
| (3n-2)(3n+1) |
| 1 |
| 3 |
| 1 |
| 3n-2 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
| n |
| 3n+1 |
| 1 |
| 4 |
| m |
| 3m+1 |
| n |
| 3n+1 |
| m |
| 3m+1 |
| 1 |
| 4 |
| n |
| 3n+1 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 3n+4 |
| n |
| 4 |
| n |
| 6m+1 |
| m2 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 13 |
| 4 |
| 3n+4 |
| n |
| 19 |
| 9 |
| 3n+4 |
| n |
| 25 |
| 16 |
| 3n+4 |
| n |
| 31 |
| 25 |
| 3n+4 |
| n |
| 37 |
| 36 |
| 3n+4 |
| n |
| lim |
| n→∞ |
| 3n+4 |
| n |
| lim |
| m→∞ |
| 6m+1 |
| m2 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 6m+1 |
| m2 |
2
| ||
| 3 |
2
| ||
| 3 |
| 13 |
| 4 |
| 3n+4 |
| n |
2
| ||
| 3 |
2
| ||
| 3 |
| 6m+1 |
| m2 |
| 3n+4 |
| n |
| 4 |
| n |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(09年山东质检理)(12分)
已知等差数列{an}的首项![]() ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
(Ⅰ)求证:数列{bn}中的每一项都是数列{an}中的项;
(Ⅱ)若a1=2,设![]() ,求数列{cn}的前n项的和Tn
,求数列{cn}的前n项的和Tn
(Ⅲ)在(Ⅱ)的条件下,若有![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年周至二中三模理) 已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2等于 ( )
(A)-4 (B)-6 (C)-8 (D)-10
查看答案和解析>>
科目:高中数学 来源:上海市普陀区高三数学高考临考自测练习卷 题型:单选题
(理)已知等差数列 的公差是
的公差是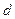 ,
, 是该数列的前
是该数列的前 项和.
项和.
(1)试用 表示
表示 ,其中
,其中 、
、 均为正整数;
均为正整数;
(2)利用(1)的结论求解:“已知
 ,求
,求 ”;
”;
(3)若数列 前
前 项的和分别为
项的和分别为
 ,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列
,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列 的前
的前 项和
项和 ,前
,前 项和
项和 ,求数列
,求数列 的前2010项的和
的前2010项的和 .”
.”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com