【题目】已知函数f（x）=lg（1+x）+lg（1﹣x）．
（1）求函数f（x）的定义域；
（2）判断函数f（x）的奇偶性；
（3）求函数f（x）的值域．
【答案】
（1）解：由 
，求得﹣1＜x＜1，
∴函数f（x）的定义域为（﹣1，1）
（2）解：定义域关于原点对称，对于任意的x∈（﹣1，1），
∵f（﹣x）=lg（1﹣x）+lg（1+x）=f（x），∴f（x）为偶函数
（3）解：f（x）=lg[（1+x）（1﹣x）]=lg（1﹣x2）．
∵t=1﹣x2 ≤1，∴y≤lg1=0，
∴函数f（x）的值域为（﹣∞，0]
【解析】（1）由 ，求得函数f（x）的定义域．（2）根据定义域关于原点对称，再根据f（﹣x）=f（x），可得f（x）为偶函数．（3）化简f（x）为lg（1﹣x2），再根据t=1﹣x2 ≤1，求得f（x）≤lg1=0，由此求得函数f（x）的值域．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝
，数列{an}满足a1＝1，an＋1＝f(an)(n∈N*)．
(1)证明数列{
}是等差数列，并求出数列{an}的通项公式；
(2)记Sn＝a1a2＋a2a3＋…＋anan＋1，求Sn．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
（
为参数， 
），其中
，在以
为极点， 
轴正半轴为极轴的极坐标系中，曲线
，曲线
.
（Ⅰ）求
与
交点的直角坐标系；
（Ⅱ）若
与
相交于点
,
与
相交于点
,求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在一次运动会中甲、乙两名射击运动员决赛中各射击十次的成绩（环）如下：
（1）用茎叶图表示甲、乙两个人的成绩；
（2）根据茎叶图分析甲、乙两人的成绩；
（3）计算两个样本的平均数
和标准差
，并根据计算结果估计哪位运动员的成绩比较稳定．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知某蔬菜商店买进的土豆
（吨）与出售天数
（天）之间的关系如表所示：
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（Ⅰ）请根据表中数据在所给网格中绘制散点图；
（Ⅱ）请根据表中提供的数据，用最小二乘法求出
关于
的线性回归方程
（其中
保留2位有效数字）；
（Ⅲ）根据（Ⅱ）中的计算结果，若该蔬菜商店买进土豆40吨，则预计可以销售多少天（计算结果保留整数）？
附：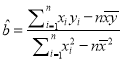 
， 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义函数y=f（x），x∈D（定义域），若存在常数C，对于任意x1∈D，存在唯一的x2∈D，使得 
=C，则称函数f（x）在D上的“均值”为C，已知f（x）=lgx，x∈[10，100]，则函数f（x）在[10，100]上的均值为（ ）
A.
B.
C.
D.10
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设关于
的一元二次方程
．
（1）若
从
， 
， 
， 
四个数中任取的一个数， 
是从
， 
， 
三个数中任取的一个数，求上述方程有实根的概率；
（2）若
是从区间
上任取的一个数， 
是从区间
上任取的一个数，求上述方程有实根的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
