
【题目】已知圆![]() 的面积为
的面积为![]() ,且与
,且与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点.
两点.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 与线段
与线段![]() 相交,求实数
相交,求实数![]() 的取值范围;
的取值范围;
(3)试讨论直线![]() 与(1)小题所求圆
与(1)小题所求圆![]() 的交点个数.
的交点个数.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)由![]() ,可得
,可得![]() ,从而可得圆
,从而可得圆![]() 的方程;(2)由(1)可得圆
的方程;(2)由(1)可得圆![]() 的方程)
的方程)![]() ,可求得
,可求得![]() 两点的坐标,根据直线
两点的坐标,根据直线![]() 与线段
与线段![]() 相交,可得到两点在直线的异侧,列不等式求解即可;(3)先求出圆心坐标及圆的半径,根据圆心到直线的距离等于、大于、小于半径可确定直线
相交,可得到两点在直线的异侧,列不等式求解即可;(3)先求出圆心坐标及圆的半径,根据圆心到直线的距离等于、大于、小于半径可确定直线![]() 与圆
与圆![]() 的交点个数.
的交点个数.
试题解析:(1)因为圆![]() :
: ![]()
![]() ,则圆的半径
,则圆的半径![]() ,
,
所以, ![]() ,即
,即![]()
所以,圆![]() 的方程为
的方程为![]() .
.
(2)因为圆![]() 的方程为
的方程为![]() ,所以,点
,所以,点![]() 、
、![]() .
.
由题意,直线![]() :
:![]() 与线段
与线段![]() 相交,
相交,
所以![]()
![]() ,解得;
,解得; ![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(3)因为圆心![]() 到直线
到直线![]() :
: ![]() 的距离
的距离![]() ,
,
当![]() ,即
,即![]() 或
或![]() 时,直线
时,直线![]() 与圆
与圆![]() 没有交点;
没有交点;
当![]() ,即
,即![]() 或
或![]() ,直线
,直线![]() 与圆
与圆![]() 有一个交点;
有一个交点;
当![]() ,即
,即![]() 时,直线
时,直线![]() 与圆
与圆![]() 有两个交点
有两个交点


科目:高中数学 来源: 题型:
【题目】下列说法中不正确的序号为_______.
①若函数![]() 在
在![]() 上单调递减,则实数
上单调递减,则实数![]() 的取值范围是
的取值范围是![]() ;
;
②函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③已知函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域是
的定义域是![]() ;
;
④若函数![]() 在
在![]() 上有最小值-4,(
上有最小值-4,(![]() ,
,![]() 为非零常数),则函数
为非零常数),则函数![]() 在
在![]() 上有最大值6.
上有最大值6.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】湖南省某自来水公司每个月(记为一个收费周期)对用户收一次水费,收费标准如下:当每户用水量不超过30吨时,按每吨2元收取;当该用户用水量超过30吨但不超过50吨时,超出部分按每吨3元收取;当该用户用水量超过50吨时,超出部分按每吨4元收取。
(1)记某用户在一个收费周期的用水量为![]() 吨,所缴水费为
吨,所缴水费为![]() 元,写出
元,写出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)在某一个收费周期内,若甲、乙两用户所缴水费的和为214元,且甲、乙两用户用水量之比为3:2,试求出甲、乙两用户在该收费周期内各自的用水量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :若关于
:若关于![]() 的方程
的方程![]() 无实数根,则
无实数根,则![]() ;命题
;命题![]() :若关于
:若关于![]() 的方程
的方程![]() 有两个不相等的正实数根,则
有两个不相等的正实数根,则![]() .
.
(1)写出命题![]() 的否命题,并判断命题
的否命题,并判断命题![]() 的真假;
的真假;
(2)判断命题“![]() 且
且![]() ”的真假,并说明理由.
”的真假,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 关于
关于![]() 轴对称,顶点在坐标原点
轴对称,顶点在坐标原点![]() ,直线
,直线![]() 经过抛物线
经过抛物线![]() 的焦点.
的焦点.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若不经过坐标原点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,且满足
,且满足![]() ,证明直线
,证明直线![]() 过
过![]() 轴上一定点
轴上一定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如下表:
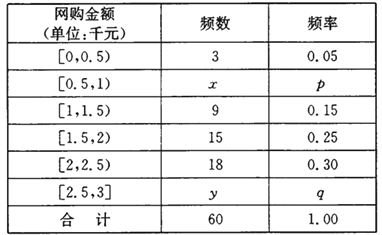
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”.已知“网购达人”与“网购探者”人数的比例为2:3.
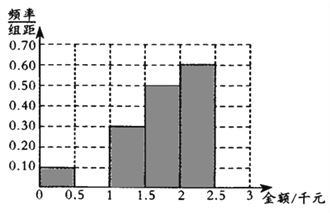
(1)确定![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日被评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点
的焦点![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若斜率![]() 的直线
的直线![]() 过抛物线的焦点
过抛物线的焦点![]() 与抛物线相交于
与抛物线相交于![]() 两点,求弦长
两点,求弦长![]() .
.
【答案】(1)![]() ;(2)8.
;(2)8.
【解析】试题分析:(1)先求圆心得焦点,根据焦点得抛物线方程(2)先根据点斜式得直线方程,与抛物线联立方程组,利用韦达定理以及弦长公式得弦长![]() .
.
试题解析:(1)圆的标准方程为![]() ,圆心坐标为
,圆心坐标为![]() ,
,
即焦点坐标为![]() ,得到抛物线
,得到抛物线![]() 的方程:
的方程: ![]()
(2)直线![]() :
: ![]() ,联立
,联立![]() ,得到
,得到![]()
弦长![]()
![]()
【题型】解答题
【结束】
19
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间和极值.
的单调区间和极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com