
【题目】某种水果按照果径大小可分为四类:标准果,优质果,精品果,礼品果.某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)用样本估计总体,果园老板提出两种购销方案给采购商参考:
方案1:不分类卖出,单价为20元/![]() .
.
方案2:分类卖出,分类后的水果售价如下表:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/ | 16 | 18 | 22 | 24 |
从采购商的角度考虑,应该采用哪种方案较好?并说明理由.
(2)从这100个水果中用分层抽样的方法抽取10个,再从抽取的10个水果中随机抽取3个,![]() 表示抽取到精品果的数量,求
表示抽取到精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)答案不唯一,见解析;(2)分布列见解析;期望为![]() .
.
【解析】
(1)计算方案2的数学期望值,与方案1比较、分析,即可得到答案;
(2)用分层抽样法求抽出精品果个数,计算对应概率值,写出分布列,求出数学期望值.
(1)解答一:设方案2的单价为![]() ,则单价的期望值为:
,则单价的期望值为:![]()
因为![]() ,
,
所以从采购商的采购资金成本角度考虑,采取方案1比较好.-
解答二:设方案2的单价为![]() ,则单价的期望值为:
,则单价的期望值为:![]()
虽然![]() ,
,![]() ,
,
但从采购商后期对水果分类的人力资源和时间成本角度考虑,采取方案2较好.
(2)用分层抽样的方法从100个水果中抽取10个,
则其中精品果4个,非精品果6个.
现从中抽取3个,则精品果的数量X服从超几何分布,
X所有可能的取值为:0,1,2,3.
则![]() ,
,![]() ,
,
![]()
![]() ,
,
所有X的分布列如下:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]()


科目:高中数学 来源: 题型:
【题目】某校李老师本学期任高一A班、B班两个班数学课教学,两个班都是50个学生,下图反映的是两个班在本学期5次数学检测中的班级平均分对比,根据图表信息,下列不正确的结论是( )

A. A班的数学成绩平均水平好于B班
B. B班的数学成绩没有A班稳定
C. 下次B班的数学平均分高于A班
D. 在第一次考试中,A、B两个班总平均分为78分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年11月26日,联合国教科文组织宣布3月14日为“国际数学日”(昵称:![]() ),2020年3月14日是第一个“国际数学日”.圆周率
),2020年3月14日是第一个“国际数学日”.圆周率![]() 是圆的周长与直径的比值,是一个在数学及物理学中普遍存在的数学常数.
是圆的周长与直径的比值,是一个在数学及物理学中普遍存在的数学常数.![]() 有许多奇妙性质,如莱布尼兹恒等式
有许多奇妙性质,如莱布尼兹恒等式![]() ,即为正奇数倒数正负交错相加等.小红设计了如图所示的程序框图,要求输出的
,即为正奇数倒数正负交错相加等.小红设计了如图所示的程序框图,要求输出的![]() 值与
值与![]() 非常近似,则①、②中分别填入的可以是( )
非常近似,则①、②中分别填入的可以是( )
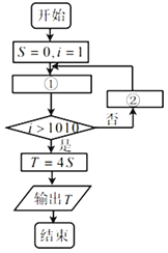
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() ,底面
,底面![]() 为平行四边形,且
为平行四边形,且![]() ,点M为
,点M为![]() 的中点,
的中点,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
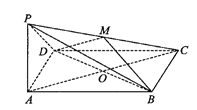
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() 时,求四棱锥
时,求四棱锥![]() 的体积及平面
的体积及平面![]() 将四棱锥分成的两部分的体积比.
将四棱锥分成的两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别是
的两个焦点分别是![]() ,直线
,直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)若![]() 为椭圆短轴上的一个顶点,且
为椭圆短轴上的一个顶点,且![]() 是直角三角形,求
是直角三角形,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥![]() 的底面正方形边长是3,
的底面正方形边长是3,![]() 是在底面上的射影,
是在底面上的射影,![]() ,
,![]() 是
是![]() 上的一点,过
上的一点,过![]() 且与
且与![]() 、
、![]() 都平行的截面为五边形
都平行的截面为五边形![]() .
.
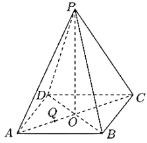
(1)在图中作出截面![]() ,并写出作图过程;
,并写出作图过程;
(2)求该截面面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点![]() 是由
是由![]() 绕直线
绕直线![]() 旋转得到,连结
旋转得到,连结![]() ,
,![]() ,
,![]() .
.
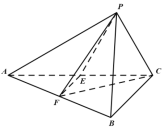
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com