
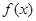 是定义在R上的奇函数,且对任意
是定义在R上的奇函数,且对任意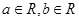 ,当
,当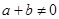 时,都有
时,都有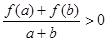 .
.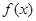 在R上为增函数.
在R上为增函数.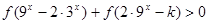 对任意
对任意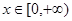 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源:不详 题型:解答题
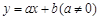 ,
,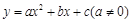 ,
,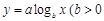 且
且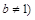 ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.| 销量t | 1 | 4 | 6 |
| 利润Q | 2 | 5 | 4.5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
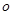 的函数关系式为:
的函数关系式为: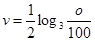 。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=
。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=| A.9 | B.8 | C.3 | D.2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且
,且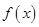 在
在 处取得极值.
处取得极值. 的值;
的值;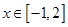 时,
时,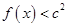 恒成立,求
恒成立,求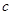 的取值范围;
的取值范围;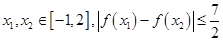 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
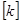 ,即
,即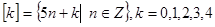 给出四个结论:
给出四个结论: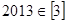 ,②
,②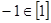 ,③
,③ ,④整数
,④整数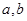 属于同一“类”,当且仅当是
属于同一“类”,当且仅当是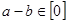 ,其中正确结论的个数是( )
,其中正确结论的个数是( )| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com