
(2)已知tanα=3,求sinα和cosα的值;
(3)已知sinα=m(|m|≤1),求cosα和tanα的值.
思路分析:(1)直接利用同角三角函数的基本关系式和角的范围求值;(2)应注意角的终边位置有两种即第一、三象限,所以结果有两种;(3)则需要分类讨论.
解:(1)因为sin2α+cos2α=1,
所以cos2α=1-sin2α=1-(![]() )2=
)2=![]() .
.
又因为α是第二象限角,所以cosα<0,
于是![]() .
.
从而![]() .
.
(2)因为sin2α+cos2α=1,所以sin2α=1-cos2α.
又因为![]() ,
,
所以![]() .
.
于是![]() ,
,![]() .
.
因为tanα=3>0,所以角α是第一或第三象限的角.
如果α是第一象限角,那么
![]() ,sinα=tanαcosα=
,sinα=tanαcosα=![]() .
.
如果α是第三象限角,那么
![]() ,sinα=tanαcosα=
,sinα=tanαcosα=![]() .
.
(3)①若m=±1,由sin2α+cos2α=1,得cos2α=1-sin2α=1-(±1)2=0,
所以cosα=0,tanα不存在.
②若m=0,则角α的终边在x轴上,由sin2α+cos2α=1,得cos2α=1-sin2α=1-02=1.
当角α的终边在x轴正半轴上时,cosα=1,tanα=0;
当角α的终边在x轴负半轴上时,cosα=-1,tanα=0.
③若0<|m|<1时,
当角α的终边在第一象限或第四象限时,由sin2α+cos2α=1,得![]() ,;
,;![]()
当角α的终边在第二象限或第三象限时,由sin2α+cos2α=1,得![]() ,
,![]() .
.
综上,可知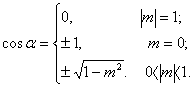
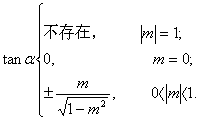
深化升华 利用同角的三角函数基本关系式,在已知一个三角函数值而求其他三角函数值时,应首先根据所给的三角函数值和已知条件判断角的终边位置,如果没法判断的话应注意分类讨论.而在具体求解时应首先利用平方关系,再利用其他关系.


科目:高中数学 来源: 题型:
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
| 1+tanα |
| 1-tanα |
| 2sinα-3cosα |
| 4sinα-9cosα |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sin(π-α)+5cos(2π-α) | ||
2sin(
|
tan(π-α)cos(2π-α)sin(-α+
| ||
| cos(-α-π)sin(-π-α) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com