
分析 (Ⅰ)过椭圆C的上顶点与右顶点的直线L为$\frac{x}{a}+\frac{y}{b}$=1,即bx+ay-ab=0.由直线L与圆x2+y2=$\frac{12}{7}$相切相切,可得$\frac{|-ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{\frac{12}{7}}$.由抛物线y2=4x的焦点为F(1,0),可得c=1.即a2-b2=1,联立解出即可得出.
(Ⅱ)当两射线与坐标轴重合时,S△OAB=$\sqrt{3}$.当两射线不与坐标轴重合时,设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),与椭圆方程联立,消去y,得(3+4k2)x2+8kmx+4m2-12=0.因为OA⊥OB,所以x1x2+y1y2=0,所以x1x2+(kx1+m)(kx2+m)=0.把根与系数的关系代入可得得7m2=12(k2+1),所以点O到直线AB的距离d=$\frac{|m|}{\sqrt{{k}^{2}+1}}$=$\sqrt{\frac{12}{7}}$.因为OA⊥OB,所以OA2+OB2=AB2≥2OA•OB,当且仅当OA=OB时,取等号.由d•AB=OA•OB,得d•|AB|=|OA|•|OB|≤$\frac{|AB{|}^{2}}{2}$,即可得出.
解答 解:(Ⅰ)过椭圆C的上顶点与右顶点的直线L为$\frac{x}{a}+\frac{y}{b}$=1,即bx+ay-ab=0.
由直线L与圆x2+y2=$\frac{12}{7}$相切相切,得$\frac{|-ab|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\sqrt{\frac{12}{7}}$.①…(1分)
因为抛物线y2=4x的焦点为F(1,0),所以c=1.…(2分)
即a2-b2=1,代入①,得7a4-31a2+12=0,
即(7a2-3)(a2-4)=0,解得a2=4,a2=$\frac{3}{7}$(舍去).…(3分)
所以b2=a2-1=3.故椭圆C的标准方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.…(4分)
(Ⅱ)当两射线与坐标轴重合时,S△OAB=$\frac{1}{2}×2×\sqrt{3}$=$\sqrt{3}$.…(5分)
当两射线不与坐标轴重合时,设直线AB的方程为y=kx+m,A(x1,y1),B(x2,y2),
与椭圆方程联立,消去y,得(3+4k2)x2+8kmx+4m2-12=0.
∴x1+x2=$\frac{-8km}{3+4{k}^{2}}$,x1•x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$.…(7分)
因为OA⊥OB,所以x1x2+y1y2=0,
所以x1x2+(kx1+m)(kx2+m)=0.
即(k2+1)x1x2+km(x1+x2)+m2=0.…(8分)
∴(k2+1)$\frac{4{m}^{2}-12}{3+4{k}^{2}}$-$\frac{8{k}^{2}{m}^{2}}{3+4{k}^{2}}$+m2=0.…(8分)
整理,得7m2=12(k2+1),
所以点O到直线AB的距离d=$\frac{|m|}{\sqrt{{k}^{2}+1}}$=$\sqrt{\frac{12}{7}}$=$\frac{2\sqrt{21}}{7}$.…(10分)
因为OA⊥OB,所以OA2+OB2=AB2≥2OA•OB,当且仅当OA=OB时,取等号.
由d•AB=OA•OB,得d•|AB|=|OA|•|OB|≤$\frac{|AB{|}^{2}}{2}$,
所以|AB|≥2d=$\frac{4\sqrt{21}}{7}$,即弦AB的长度的最小值是$\frac{4\sqrt{21}}{7}$.
所以△OAB的最小面积为S△OAB=$\frac{1}{2}×\frac{4\sqrt{21}}{7}$×$\frac{2\sqrt{21}}{7}$=$\frac{12}{7}$.
综上,△OAB面积的最小值为$\frac{12}{7}$.…(12分)
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、三角形面积计算公式、一元二次方程的根与系数的关系、点到直线的距离公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
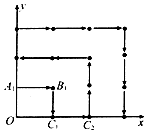 某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )| A. | 1936 | B. | 2016 | C. | 2017 | D. | 2208 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
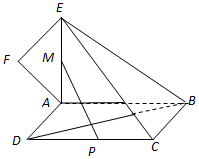 如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
如图,正方形ABCD所在平面与四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2tanα | B. | 2tanα | C. | $\frac{-2}{tanα}$ | D. | $\frac{2}{tanα}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com